Брусок — сколько в кубе штук
При подготовке к строительству деревянного здания, дома или постройки будет рассудительнее предварительно узнать общее количество необходимого материала для полного завершения строительства объекта. А когда в процессе используется брусок, то его количество можно узнать при помощи специальных таблиц с расчетами. Или же для этого можно воспользоваться расчетами, проведенными самостоятельными силами.
|
ТОЛЬКО ЛУЧШИЕ ПИЛОМАТЕРИАЛЫ
|
БЕСПЛАТНАЯ ПОГРУЗКА
|
|
ОПЕРАТИВНАЯ ДОСТАВКА ПО МОСКВЕ И ОБЛАСТИ
|
ОПЛАТА КАК НАЛИЧНЫМИ, ТАК И ПО БЕЗНАЛУ!
|
|
ГАРАНТИЯ БЕРЕЖНОГО ХРАНЕНИЯ
|
СКИДКИ ОПТОВЫМ ПОКУПАТЕЛЯМ
|
Основной способ подсчета количества бруска в кубе древесины заключается в простой формуле, для этого необходимо площадь прямоугольного поперечника бруска умножить на его длину, а сам поперечник вычисляется умножением высоты на ширину.
Для точного определения количества бруска в кубическом метре древесины, в зависимости от его поперечного сечения и длинны, необходимо произвести расчеты:
Например, для строительства объекта необходимо 100 погонных метров бруска марки 40 на 50 мм, который имеет длину 3 метра. Для этого сначала необходимо узнать площадь его поперечника: 0,04 м * 0,05 м = 0,002 кв. м., она оставляет 0,002 кв. м. Далее необходимо эту площадь умножить на длину бруска: 0,002 * 3 = 0,006 куб. м. – это объем одного бруска с поперечником 40 на 50 мм. Потом делим 1 кубический метр древесины на объем одного бруска: 1 куб. м. / 0,006 куб. м. = 166 штук.
Вот теперь имеется полученный результат, всего 166 штук бруска в 1-ом (одном) кубическом метре древесины с поперечником 40 на 50 мм и длинной 3 метра. Теперь каждый сможет узнать про брусок – сколько в кубе будет штук брусков. По такой же аналогичной формуле можно производить расчеты количества бруска относительно других видов бруска, имеющего разные показатели и размеры поперечника.
Подсчеты и завершение математической задачи
Из примера, теперь можно подсчитать, что для строительства объекта необходимо будет 100 п. м.* 0,006 куб. м. = 0,6 куб. м. Вот тоже получен результат, для полного завершения строительства объекта, для которого необходимо 100 погонных метров бруска, необходимо купить 0,6 кубических метров древесины. Эта цифра понадобится для пересчета стоимости бруска, купленного поштучно за единицу изделия на стоимость одного куба древесины.
Таблица количества бруска в кубе
| Наименование пиломатериала | Размер сечений бруса (мм) | Сколько бруса (штук) в кубе (в 1 куб. метре) | Объем одного бруса в кубических метрах (м3) |
| Брусок | 25х50х3000 | 266 | 0,0037 |
| Брусок | 30х40х3000 | 277 | 0,0036 |
| Брусок | 30х50х3000 | 222 | 0,0045 |
| Брусок | 40х40х3000 | 208 | 0,0048 |
| Брусок | 50х50х3000 | 133 | 0,0075 |
| Брусок | 50х70х3000 | 95 | 0,01 |
Сколько штук бруса в кубе: таблица-кубатурник для расчета цены
Куб бруса: сколько в нем отдельных штук пиломатериала (формула расчета)
Для того, что бы рассчитать брус в кубах или штуках, используется либо готовая таблица-кубатурник, либо формула расчета куба бруса в штуках: 1 кубический метр нужно разделить на объем одного бруса заданного размера.
То есть, вам сначала необходимо рассчитать объем одного бруса по формуле V = a * b * l (здесь V – объем в метрах , м³; a – высота, м; b – ширина, м; l – длина, м). Так же объемы 1 штуки указаны в таблице 2 . Можете поверить, а можно и проверить. Длина чаще всего составляет 6 метров, или 6000 мм. Чтобы самостоятельно определить какой объем у брусьев определенного сечения, необходимо знать длину, ширину и высоту.
К примеру, если у вас будет использоваться брус размером сто на сто, то мы проводим следующие расчеты.
Один брус размером 100х100 занимает такой объем: 100мм · 100мм · 6000 мм = 0,1м · 0,1м · 6м = 0,06 м3.
1куб бруса 100*100 займет 0,06 м3 .
Второй шаг определяет непосредственно количество бруса 100х100 в одном кубе с помощью формулы расчета бруса в штуках: 1м3 / 0,06м3 = 16,67 шт./м3. Дальше округляем полученное значение , лучше в большую сторону, чем по правилам математики.
Необходимое количество можно посчитать, используя таблицы пилорамы «78 Досок». Купить брус или посмотреть актуальные цены на пиломатериалы можно используя каталог пиломатериалов по этой ссылке.
Таблица кубатурник бруса
| Размер бруса (мм) | Объем 1-го бруса | Штук бруса в 1-ом кубе |
|---|---|---|
| 100х100х6000 | 0,06 м³ | 16,67 штук |
| 100х150х6000 | 0,09 м³ | 11,11 штук |
| 150х150х6000 | 0,135 м³ | 7,41 штук |
| 100х180х6000 | 0,108 м³ | 9,25 штук |
| 150х180х6000 | 0,162 м³ | 6,17 штук |
| 180х180х6000 | 0,1944 м³ | 5,14 штук |
| 100х200х6000 | 0,12 м³ | 8,33 штук |
| 150х200х6000 | 0,18 м³ | 5,55 штук |
| 180х200х6000 | 0,216 м³ | 4,62 штук |
| 200х200х6000 | 0,24 м³ | 4,16 штук |
| 250х200х6000 | 0,3 м³ | 3,33 штук |
| 250х250х6000 | 0,375 м³ | 2,66 штук |
| 250х300х6000 | 0,45 м³ | 2,22 штук |
| 300х300х6000 | 0,54 м³ | 1,85 штук |
Объем одной штуки бруса длиной 6 метров
| Размер бруса | Объем 1-й штуки |
|---|---|
| 100х100х6000 | 0,06 м³ |
| 100х150х6000 | 0,09 м³ |
| 150х150х6000 | 0,135 м³ |
| 100х180х6000 | 0,108 м³ |
| 150х180х6000 | 0,162 м³ |
| 180х180х6000 | 0,1944 м³ |
| 100х200х6000 | 0,12 м³ |
| 150х200х6000 | 0,18 м³ |
| 180х200х6000 | 0,216 м³ |
| 200х200х6000 | 0,24 м³ |
| 250х200х6000 | 0,3 м³ |
| 250х250х6000 | 0,375 м³ |
| 250х300х6000 | 0,45 м³ |
| 300х300х6000 | 0,54 м³ |
| Размер бруса | Количество штук бруса в кубе |
|---|---|
| 40х50х6000 | 83,3 штук |
| 50х50х6000 | 66. 66 штук 66 штук |
| 100х100х6000 | 16.66 штук |
| 100х150х6000 | 11.11штук |
| 100х200х6000 | 8.33 штук |
| 150х150х6000 | 7.4 штук |
| 150х200х6000 | 5.55 штук |
| 200х200х6000 | 4.16 штук |
формула расчета строительного материала
Брус 100х100 мм широко и успешно применяется во многих сферах человеческой деятельности. Коммерческое строительство, а также возведение конструктивных систем личного назначения не обходится без использования профилированного бруса. Качество материала проверено годами. Деревянный брус имеет повышенные эксплуатационные характеристики за счет специальной обработки в процессе производства, что значительно увеличивает срок службы изделий, построенных из дерева. Для того, чтобы приступить к закупке материала и строительным работам, в дальнейшем необходимо рассчитать необходимое количество материала и знать сколько пиломатериалов в 1м 3 .
Правила расчета материала и его расхода
Таким способом можно рассчитать точное количество брусков в упаковке при различном сечении изделий. Все, что требуется для расчета – это знание простых правил математики и параметров деревянных брусков.
Рассчитать, сколько брусков в кубе 100х100 мм, не составит труда, зная специальную формулу.
Для расчета необходима длина изделия, например, строительный брус длиной 5 метров укладывается таким образом, чтобы изделия плотно прилегали друг к другу, а их сечения образовывали метр квадратный.
С учетом того, что параметры изделия 100х100 мм, получается стопка из дерева 10х10. Умножив количество, получим пучок пиломатериалов в количестве ста штук.
Так как брусок имеет длину 5 метров, а вы хотите узнать, сколько брусков в кубе 100х100, вам нужно вычислить 1/5 от общего количества бруска: 100/5 = 20.
Особенности расчет
Если расчет выдает число со знаками после запятой, нет смысла его округлять, иначе нечем будет восполнить пробел в случае дефицита материала. Ответ на вопрос о том, сколько брусков в кубе 100х100, дает именно расчет.
Ответ на вопрос о том, сколько брусков в кубе 100х100, дает именно расчет.
Как видите расчеты не сложные, их легко провести самостоятельно и своими руками. Если человек, занимающийся строительством, поймет, сколько пиломатериалов в кубе 100х100, проанализирует цены на продукцию и будет знаком с характеристиками пород деревьев, выбрать хороший материал и совершить точную покупку будет намного проще.
Как правильно закупить материал
Закупка пиломатериала осуществляется оптом в кубометрах. Знание формул и таблиц расчета стройматериалов поможет существенно сэкономить бюджет строительства. Сегодня на рынке строительных материалов в России много древесины. Древесина – ценный материал, соответственно и цена куба бруса высокая. Согласно анализу рынка за 2015 год, кубометр строганного профилированного материала стоит до 5 500 рублей. Сегодня эта цифра увеличилась и у некоторых производителей достигает 7000 рублей за куб пиломатериала.
Некоторые производители при крупнооптовых закупках предлагают покупателю скидку, что позволяет сэкономить на покупке материала.
Иногда в Интернете предлагаются по дешевке продажи профилированного бруса, но такие позиции не всегда отличаются качеством продукции, ведь бесплатный сыр — только в мышеловке. Поэтому бар лучше заказывать лично на базе, видя товар перед собой.
Расчет планки дело точное, поэтому при проведении подобных операций будьте предельно внимательны, чтобы правильно произвести расчет.
Звезды и полосы
\(\def\d{\displaystyle}
\def\курс{Математика 228}
\ новая команда {\ f} [1] {\ mathfrak # 1}
\ новая команда {\ s} [1] {\ mathscr # 1}
\def\N{\mathbb N}
\def\B{\mathbf{B}}
\def\circleA{(-.5,0) круг (1)}
\ деф \ Z {\ mathbb Z}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\Q{\mathbb Q}
\def\circleB{(.5,0) круг (1)}
\def\R{\mathbb R}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\C{\mathbb C}
\def\circleC{(0,-1) круг (1)}
\def\F{\mathbb F}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\А{\mathbb А}
\def\twosetbox{(-2,-1.5) прямоугольник (2,1.5)}
\ деф \ Х {\ mathbb Х}
\def\threesetbox{(-2,-2. {-1}}
{-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-. 5,0) круг (1)}
5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\renewcommand{\bar}{\overline}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
¶
Расследуй!10
Предположим, у вас есть некоторое количество одинаковых кубиков Рубика, которые вы хотите раздать своим друзьям. Представьте, что вы начинаете с одного ряда кубиков.
Представьте, что вы начинаете с одного ряда кубиков.
Найдите количество различных способов, которыми вы можете распределить предоставленные кубики:
У вас есть 3 кубика, которые нужно раздать 2 людям.
У вас есть 4 кубика, которые нужно раздать 2 людям.
У вас есть 5 кубиков, которые нужно раздать 2 людям.
У вас есть 3 кубика, которые нужно раздать трем людям.
У вас есть 4 кубика, которые нужно раздать трем людям.
У вас есть 5 кубиков, которые нужно раздать трем людям.
Предположите, сколькими способами можно раздать 7 кубиков 4 людям. Объяснять.
Что, если бы каждый человек должен был получить хотя бы один кубик ? Как бы изменились ваши ответы?
Рассмотрим следующую задачу на подсчет:
У вас есть 7 печенек, которые нужно отдать 4 детям. Сколько способов вы можете сделать это?
Подумайте, как вы могли бы решить эту проблему.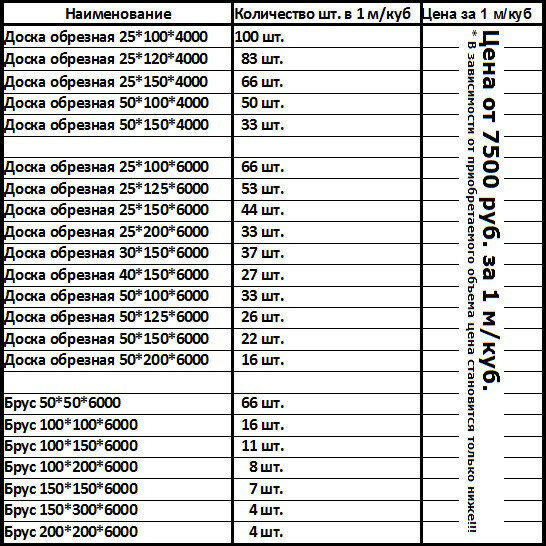 7\text{,}\), потому что здесь порядок равен не имеет значение. На самом деле другой способ записать тот же результат —
7\text{,}\), потому что здесь порядок равен не имеет значение. На самом деле другой способ записать тот же результат —
.
\begin{уравнение*}
\mbox{AAABCDD} .
\end{уравнение*}
Это будет предпочтительное представление результата. Поскольку мы можем писать буквы в любом порядке, мы могли бы также написать их в алфавитном порядке для целей подсчета. Итак, сначала мы напишем все буквы А, затем все буквы Б и так далее.
Теперь подумайте, как вы могли бы определить такой результат. Все, что нам действительно нужно сделать, это сказать, когда переходить от одной буквы к другой. Что касается куки-файлов, нам нужно сказать, через сколько куки-файлов мы прекращаем давать куки-файлы первому ребенку и начинаем давать куки-файлы второму ребенку. А потом через сколько переходим на третьего пацана? А через сколько переходим на четвертую? Итак, еще один способ представления результата выглядит следующим образом:
\begin{уравнение*}
***|*|*|**
\end{уравнение*}
Первому ребёнку идёт три печенья, потом меняем и даем одно печенье второму ребёнку, потом меняем, одно третьему ребёнку, меняем, два четвёртому ребёнку. Обратите внимание, что нам нужно 7 звездочек и 3 полоски — по одной звездочке на каждое печенье и по одной полоске на каждое переключение между дочерними элементами, поэтому на одну полоску меньше, чем детей (нам не нужно переключаться после последнего дочернего элемента — мы закончили) .
Обратите внимание, что нам нужно 7 звездочек и 3 полоски — по одной звездочке на каждое печенье и по одной полоске на каждое переключение между дочерними элементами, поэтому на одну полоску меньше, чем детей (нам не нужно переключаться после последнего дочернего элемента — мы закончили) .
Зачем мы все это сделали? Все просто: чтобы посчитать, сколько способов раздать 7 печений 4 детям, нам нужно только посчитать, сколько звезд и баров графиков есть. Но диаграмма звезд и баров — это просто набор символов, несколько звезд и несколько баров. Если бы вместо звездочек и полос мы использовали 0 и 1, это была бы просто битовая строка. Мы умеем их считать.
Прежде чем мы будем слишком волноваться, мы должны убедиться, что действительно любая строка (в нашем случае) из 7 звезд и 3 полосок соответствует другому способу раздачи печенья детям. В частности, рассмотрим такую строку:
.
\begin{уравнение*}
|***||****
\end{уравнение*}
Соответствует ли это распространению файлов cookie? Да.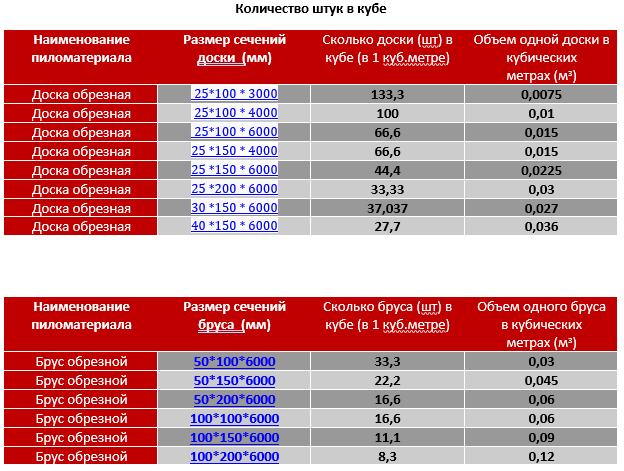 Он представляет собой распределение, при котором ребенок А получает 0 печенек (потому что мы переключаемся на ребенка Б до того, как появятся звездочки), ребенок Б получает три куки (три звездочки перед следующей полоской), ребенок С получает 0 печенек (без звездочек перед следующей полоской). а ребенок D получает оставшиеся 4 печенья. Независимо от того, как расположены звезды и полосы, мы можем распространять файлы cookie таким образом. Кроме того, при любом способе распространения файлов cookie мы можем представить это с помощью диаграммы звезд и столбцов. Например, распределение, при котором ребенок А получает 6 печений, а ребенок Б получает 1 печенье, имеет следующую диаграмму:
Он представляет собой распределение, при котором ребенок А получает 0 печенек (потому что мы переключаемся на ребенка Б до того, как появятся звездочки), ребенок Б получает три куки (три звездочки перед следующей полоской), ребенок С получает 0 печенек (без звездочек перед следующей полоской). а ребенок D получает оставшиеся 4 печенья. Независимо от того, как расположены звезды и полосы, мы можем распространять файлы cookie таким образом. Кроме того, при любом способе распространения файлов cookie мы можем представить это с помощью диаграммы звезд и столбцов. Например, распределение, при котором ребенок А получает 6 печений, а ребенок Б получает 1 печенье, имеет следующую диаграмму:
\begin{уравнение*}
******|*||
\end{уравнение*}
После всей этой работы мы, наконец, готовы к подсчету. Каждый способ распространения файлов cookie соответствует диаграмме звезд и столбцов с 7 звездами и 3 столбцами. Итак, есть 10 символов, и мы должны выбрать 3 из них в качестве баров. Таким образом:
\begin{уравнение*}
\mbox{ Существует } {10 \выберите 3}\mbox{ способов раздать 7 файлов cookie 4 детям. }
}
\end{уравнение*}
Пока мы здесь, мы можем также ответить на родственный вопрос: сколько существует способов раздать 7 печений 4 детям так, чтобы каждый ребенок получил хотя бы одно печенье? Что вы можете сказать о соответствующих звездочках и гистограммах? Графики должны начинаться и заканчиваться хотя бы одной звездочкой (чтобы дети A и D) получали печенье, а также никакие две полоски не могли быть соседними (чтобы дети B и C не были пропущены). Один из способов обеспечить это — размещать полосы только в местах 9.0079 между звездами. При 7 звездах между звездами 6 точек, поэтому мы должны выбрать 3 из этих 6 точек, чтобы заполнить их полосами. Таким образом, есть \({6 \выбрать 3}\) способов раздать 7 печенек 4 детям, дав хотя бы по одной печенюшке каждому ребенку.
Другой (и более общий) способ решить эту модифицированную задачу — сначала дать каждому ребенку по одному печенью. Теперь оставшиеся 3 печенья можно раздать 4 детям без ограничений. Итак, у нас есть 3 звезды и 3 полосы, всего 6 символов, 3 из которых должны быть полосами. Итак, мы снова видим, что существует \({6 \выберите 3}\) способов распространения файлов cookie.
Итак, мы снова видим, что существует \({6 \выберите 3}\) способов распространения файлов cookie.
Звездочки и полоски можно использовать для решения задач, отличных от детей и печенья. Вот несколько примеров:
Пример 1.5.1
Ваша любимая математическая сеть пиццерий предлагает 10 начинок. Сколько пицц можно приготовить, если разрешено 6 начинок? Порядок начинки не имеет значения, но теперь вам разрешены повторы. Таким образом, одна из возможных пицц — это тройная колбаса, двойной ананас и лук.
Solution
Получаем 6 начинок (с учетом возможных повторов). Представьте каждую из этих начинок в виде звезды. Подумайте о том, чтобы идти по меню по одной начинке за раз: сначала вы видите анчоусы, а затем переходите к следующей, колбасе. Вы говорите «да» колбасе 3 раза (используйте 3 звезды), затем переключаетесь на следующую начинку в списке. Вы продолжаете пропускать, пока не дойдете до ананаса, на который дважды соглашаетесь.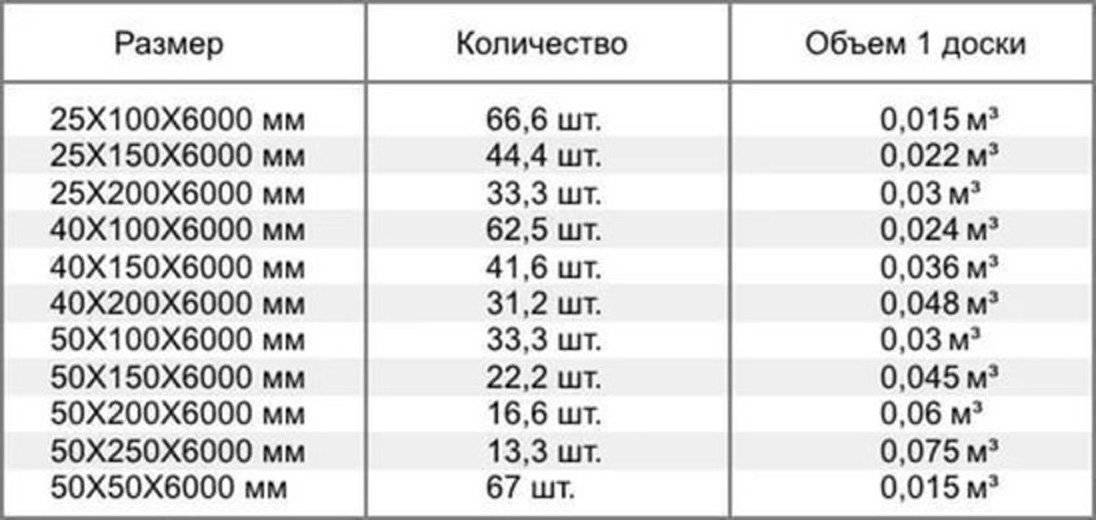 Еще один переключатель, и вы у лука. Вы говорите «да» один раз. Затем вы продолжаете переключаться, пока не дойдете до последней начинки, больше никогда не говоря «да» (поскольку вы уже сказали «да» 6 раз. На выбор 10 начинок, поэтому надо переключаться с рассмотрения одной начинки на следующие 9раз. Это бары.
Еще один переключатель, и вы у лука. Вы говорите «да» один раз. Затем вы продолжаете переключаться, пока не дойдете до последней начинки, больше никогда не говоря «да» (поскольку вы уже сказали «да» 6 раз. На выбор 10 начинок, поэтому надо переключаться с рассмотрения одной начинки на следующие 9раз. Это бары.
Теперь, когда мы уверены, что у нас правильное количество звездочек и полосок, отвечаем на вопрос просто: звездочек 6 и полосок 9, значит, 15 символов. Нам нужно выбрать 9 из них, чтобы они были барами, поэтому возможное количество пицц равно
.
\begin{уравнение*}
{15 \ выберите 9}.
\end{уравнение*}
Пример 1.5.2
Сколько существует семизначных телефонных номеров, в которых цифры не возрастают? То есть каждая цифра меньше или равна предыдущей.
Решение
Нам нужно выбрать 7 цифр, поэтому мы будем использовать 7 звезд. Полосы будут представлять собой переход от каждого возможного однозначного числа к следующему меньшему числу. Таким образом, номер телефона 866-5221 представлен диаграммой звезд и столбцов
Таким образом, номер телефона 866-5221 представлен диаграммой звезд и столбцов
.
\begin{уравнение*}
|*||**|*|||**|*|
\end{уравнение*}
Для каждой цифры (0-9) есть 10 вариантов, поэтому мы должны переключаться между вариантами 9 раз. У нас 7 звездочек и 9 полосок, поэтому общее количество телефонных номеров
\begin{уравнение*}
{16 \ выберите 9}.
\end{уравнение*}
Пример 1.5.3
Сколько целочисленных решений есть у уравнения
\begin{уравнение*}
х_1 + х_2 + х_3 + х_4 + х_5 = 13.
\end{уравнение*}
( целочисленное решение уравнения — это решение, в котором неизвестное должно иметь целочисленное значение.)
где \(x_i \ge 0\) для каждого \(x_i\text{?}\)
где \(x_i > 0\) для каждого \(x_i\text{?}\)
где \(x_i \ge 2\) для каждого \(x_i\text{?}\)
Решение
Эта задача аналогична раздаче 13 печенек пятерым детям. Нам нужно сказать, сколько из 13 единиц приходится на каждую из 5 переменных. Другими словами, у нас есть 13 звездочек и 4 полосы (полосы похожи на знаки «+» в уравнении).
Нам нужно сказать, сколько из 13 единиц приходится на каждую из 5 переменных. Другими словами, у нас есть 13 звездочек и 4 полосы (полосы похожи на знаки «+» в уравнении).
Если \(x_i\) может быть 0 или больше, мы находимся в стандартном случае без ограничений. Таким образом, 13 звезд и 4 полоски можно расположить \({17 \выбрать 4}\) способами.
Теперь каждая переменная должна быть не меньше 1. Поэтому дайте одну единицу каждой переменной, чтобы удовлетворить этому ограничению. Теперь осталось 8 звездочек и еще 4 полоски, поэтому число решений равно \({12 \выбрать 4}\text{.}\)
Теперь каждая переменная должна быть 2 или больше. Итак, перед любым подсчетом дайте каждой переменной 2 единицы. Теперь у нас осталось 3 звездочки и 4 полоски, значит, есть \({7 \выбрать 4}\) решений.
Счет с функциями
Многие задачи на подсчет в этом разделе могут на первый взгляд показаться примерами подсчета функций .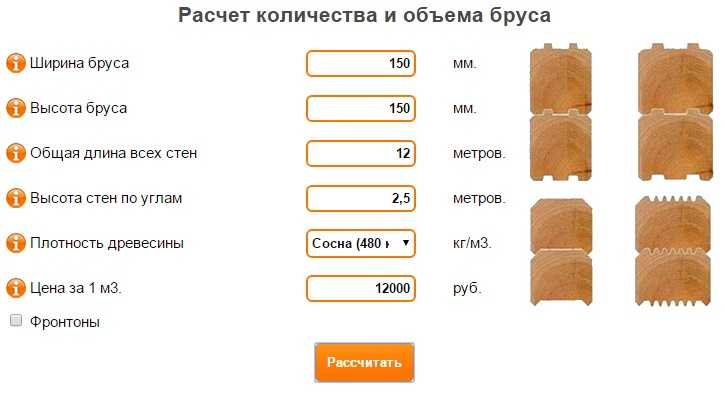 7 = 16384\text{.}\) Что здесь происходит?
7 = 16384\text{.}\) Что здесь происходит?
Когда мы считаем функции, мы считаем, например, следующие две функции разными:
\begin{уравнение*}
f = \twoline{1 \amp 2 \amp 3 \amp 4\amp 5 \amp 6 \amp 7}{a \amp b \amp c \amp c \amp c \amp c \amp c} \qquad g = \twoline{1 \amp 2 \amp 3 \amp 4\amp 5 \amp 6 \amp 7}{b \amp a \amp c \amp c \amp c \amp c \amp c}.
\end{уравнение*}
Но эти две функции будут соответствовать тому же распределению файлов cookie : дети \(a\) и \(b\) получают по одному файлу cookie, ребенок \(c\) получает остальные (и ничего для ребенка \(d\). )).
Дело в том, что элементы домена различимы, куки неразличимы. Это аналогично различию между перестановками (например, счетными функциями) и комбинациями (нет).
ПодразделУпражнения
¶
1
Мультимножество — это набор объектов, такой же, как набор, но может содержать объект более одного раза (порядок элементов при этом не имеет значения). Например, \(\{1,1, 2, 5, 5, 7\}\) — это мультимножество размера 6.
Например, \(\{1,1, 2, 5, 5, 7\}\) — это мультимножество размера 6.
Сколько наборов размера 5 можно составить, используя 10 цифр от 0 до 9?
Сколько наборов multi размера 5 можно составить, используя 10 цифр от 0 до 9?
Решение
- \({10\выберите 5}\) наборов. Мы должны выбрать 5 из 10 цифр, чтобы поместить их в набор.
Используйте звездочки и полосы: каждая звездочка представляет один из 5 элементов набора, каждая полоса представляет собой переключение между цифрами. Так что есть 5 звезд и 9баров, что дает нам \({14 \выбрать 9}\) наборов.
2
Каждую из приведенных ниже задач на счет можно решить с помощью звездочек и полосок. Для каждого скажите, какой исход диаграммы
\begin{уравнение*}
***|*||**|
\end{уравнение*}
показывает, правильное ли количество звездочек и полосок соответствует задаче. В противном случае скажите, почему диаграмма не представляет никакого результата и как должна выглядеть правильная диаграмма.
Сколькими способами можно выбрать горсть 6 мармеладок из банки с 5 разными вкусами?
Сколькими способами можно раздать 5 одинаковых леденцов 6 детям?
Сколько слов из 6 букв можно составить, используя 5 гласных?
Сколько решений есть у уравнения \(x_1 + x_2 + x_3 + x_4 = 6\text{.}\)
Решение
Вы берете 3 клубники, 1 лайм, 0 солодки, 2 черники и 0 жевательной резинки.
Это наоборот. Мы не хотим, чтобы звезды представляли детей, потому что дети не идентичны, но звезды идентичны. Вместо этого мы должны использовать 5 звезд (для леденцов) и использовать 5 полосок для переключения между 6 детьми. Например,
\begin{уравнение*}
**||***|||
\end{уравнение*}
Числобудет означать, что первый ребенок получит 2 леденца, третий — 3, а остальные — ни одного.
Это слово АААЕОО.
Это не решение.
 Каждая звездочка должна представлять одну из 6 единиц, которые в сумме дают 6, а столбики должны переключаться между различными переменными. У нас слишком много баров. Пример правильной диаграммы будет
Каждая звездочка должна представлять одну из 6 единиц, которые в сумме дают 6, а столбики должны переключаться между различными переменными. У нас слишком много баров. Пример правильной диаграммы будет\begin{уравнение*}
*|**||***,
\end{уравнение*}, что означает, что \(x_1 = 1\text{,}\) \(x_2 = 2\text{,}\) \(x_3 = 0\text{,}\) и \(x_4 = 3\text{.} \)
3
После урока физкультуры вам нужно разложить 14 одинаковых вышибалов по 5 корзинам.
Сколькими способами можно это сделать, если нет ограничений?
Сколькими способами можно это сделать, если в каждой ячейке должен быть хотя бы один вышибалы?
Решение
- \({18 \выбрать 4}\) способов. Каждый результат может быть представлен последовательностью из 14 звездочек и 4 полосок.
- \({13 \выбрать 4}\) способов. Сначала положите по одному мячу в каждую корзину. Это оставляет 9 звезд и 4 полоски.
4
Сколько целочисленных решений уравнения \(x + y + z = 8\), для которого
- \(x\text{,}\) \(y\text{,}\) и \(z\) все положительны?
- \(x\text{,}\) \(y\text{,}\) и \(z\) неотрицательны?
- \(x\text{,}\) \(y\text{,}\) и \(z\) больше, чем \(-3\text{.
 }\)
}\)
Решение
- \({7 \выберите 2}\) решения. После того, как каждая переменная получает 1 звезду бесплатно, у нас остается 5 звезд и 2 полоски.
- \({10 \выберите 2}\) решений. У нас есть 8 звезд и 2 бара.
- \({19 \выбрать 2}\) решений. Эта задача эквивалентна нахождению числа решений \(x’ + y’ + z’ = 17\), где \(x’\text{,}\) \(y’\) и \(z’\) неотрицательны. (На самом деле мы просто делаем замену. Пусть \(x = x’- 3\text{,}\) \(y = y’-3\) и \(z = z’-3\)).
5
Используя цифры от 2 до 8, найдите количество различных пятизначных чисел, таких что:
Цифры не могут повторяться и должны быть записаны в порядке возрастания. Например, 23678 — это нормально, а 32678 — нет.
Цифры могут повторяться и должны быть записаны в неубывающем порядке. Например, 24448 — это нормально, а 24484 — нет.
Решение
Есть \({7 \выберите 5}\) чисел.
 Мы просто выбираем пять из семи цифр и после выбора ставим их в порядке возрастания.
Мы просто выбираем пять из семи цифр и после выбора ставим их в порядке возрастания.Для этого требуются звезды и полосы. Используйте звездочку, чтобы представить каждую из 5 цифр в числе, и используйте их положение относительно полос, чтобы сказать, какая цифра заполняет это место. Таким образом, у нас будет 5 звездочек и 6 полосок, что дает \({11 \выбрать 6}\) чисел.
6
Играя в Ятзи, вы бросаете пять обычных шестигранных кубиков. Сколько различных исходов возможно из одного броска? Порядок кубиков не имеет значения.
7
Ваша подруга говорит вам, что у нее в руке 7 монет (только пенни, пятаки, десять центов и четвертак). Если вы угадаете, сколько у нее монет каждого вида, она даст их вам. Если вы угадаете наугад, какова вероятность того, что вы окажетесь правы?
8
Сколько существует целочисленных решений \(x_1 + x_2 + x_3 + x_4 = 25\), для которых \(x_1 \ge 1\text{,}\) \(x_2 \ge 2\text{,}\) \ (x_3 \ge 3\) и \(x_4 \ge 4\text{?}\)
9
Решите три задачи на подсчет ниже.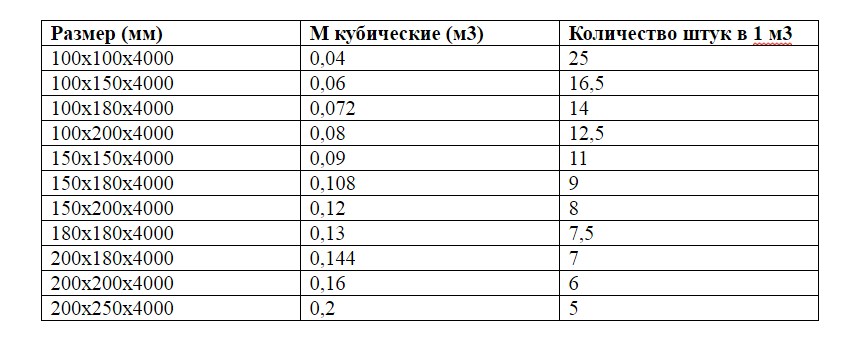 Затем скажите, почему логично, что у всех один и тот же ответ. То есть сказать, как вы можете интерпретировать их как друг друга.
Затем скажите, почему логично, что у всех один и тот же ответ. То есть сказать, как вы можете интерпретировать их как друг друга.
Сколько существует способов раздать 8 печений трем детям?
Сколько существует решений в неотрицательных целых числах для \(x+y+z = 8\text{?}\)
Сколько разных упаковок по 8 мелков можно сделать, используя мелки красного, синего и желтого цветов?
10
Рассмотрим функции \(f:\{1,2,3,4,5\} \to \{0,1,2,\ldots,9\}\text{.}\)
Сколько из этих функций строго возрастают? Объяснять. (Функция строго возрастает, если \(a \lt b\text{,}\), то \(f(a) \lt f(b)\text{.}\))
Сколько функций неубывающих? Объяснять. (Функция неубывающая, если \(a \lt b\text{,}\), то \(f(a) \le f(b)\text{.}\))
11
Conic , ваш любимый ресторан быстрого питания с математической тематикой предлагает 20 вкусов, которые можно добавить в газировку.

 Каждая звездочка должна представлять одну из 6 единиц, которые в сумме дают 6, а столбики должны переключаться между различными переменными. У нас слишком много баров. Пример правильной диаграммы будет
Каждая звездочка должна представлять одну из 6 единиц, которые в сумме дают 6, а столбики должны переключаться между различными переменными. У нас слишком много баров. Пример правильной диаграммы будет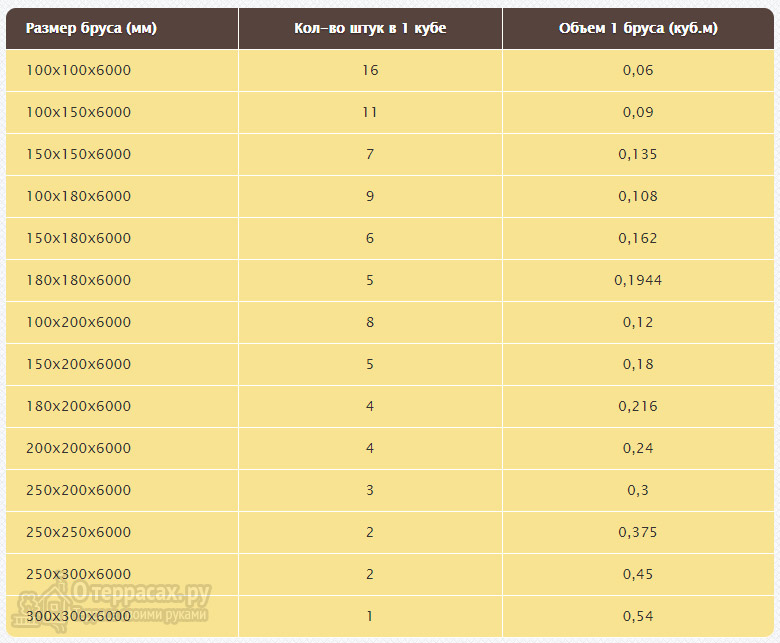 }\)
}\) Мы просто выбираем пять из семи цифр и после выбора ставим их в порядке возрастания.
Мы просто выбираем пять из семи цифр и после выбора ставим их в порядке возрастания.