Калькулятор площади стен в квадратных метрах
🕒
  👁 1 407
Перед вами онлайн калькулятор для расчета площади стен в квадратных метрах (м2). Он необходим, например, при вычислении требуемого количества строительных материалов для комнаты. Стены могут штукатуриться, утепляться, оклеиваться обоями или красится. Вот для этого и нужно точно знать общую площадь стены, а иногда и периметр.
Ширина помещения   B
ммсмм
Длина помещения   L
ммсмм
Высота помещения   H
ммсмм
Площадь стен   S
мм²см²м²
Периметр стен   P
ммсмм
Расчет площади стен на нашем калькуляторе делается элементарно. Просто введите размеры помещения (ширину и длину), выберите единицы измерения и нажмите на кнопку «Рассчитать».
Сразу же будет вычислена общая площадь в квадратных метрах или в других размерностях по вашему выбору. В дополнение будет рассчитан периметр всех стен. Это например пригодится для определения необходимого количества плинтуса.
В дополнение будет рассчитан периметр всех стен. Это например пригодится для определения необходимого количества плинтуса.
Кому дополнительно ещё нужно будет рассчитать площадь потолка или пола, попробуйте также наш калькулятор помещения.
И помните: наш онлайн-калькулятор делает расчет площади стен только для прямоугольной комнаты, ну или квадратной. Если помещение составное, то его нужно делить на простые фигуры и для каждой его части отдельно определять площадь путем перемножения длины стены на её высоту.
Чтобы рассчитать площадь стен комнаты по формуле достаточно просто знать её размеры. Формула расчета площади стен выглядит следующим образом:
S = 2 * (B + L) * H , где
B — ширина помещения,
L — длина помещения,
H — высота помещения.
Рассмотрим как вычислить площадь стен комнаты на простейшем примере.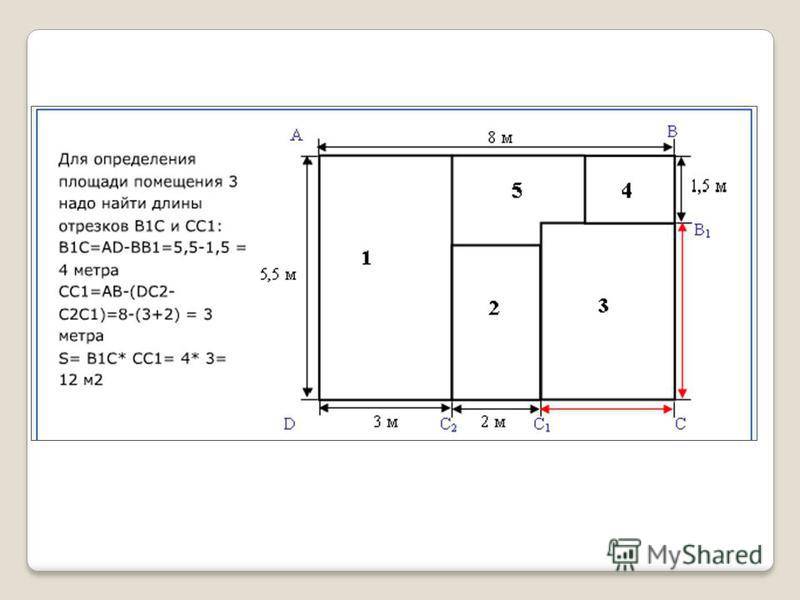 Пусть у нас есть следующие размеры: ширина комнаты 4 метра, длина комнаты 5 метров, а её высота составляет 3 метра. В примере не будем учитывать окна и двери.
Пусть у нас есть следующие размеры: ширина комнаты 4 метра, длина комнаты 5 метров, а её высота составляет 3 метра. В примере не будем учитывать окна и двери.
Подставим имеющиеся данные в формулу площади и вручную получим результат.
S = 2 * (4 + 5) * 3 = 54,00 м2.
Если в помещении есть окна и двери, то от общей площади стен нужно вычесть площадь всех имеющихся окон и дверей. Тогда мы получим площадь стен с учётом проёмов в них.
Как находится периметр комнаты показывать не будем. Это для вас скажем так домашняя задачка будет.
Вот мы и разобрали один из наиболее частых вопросов в строительстве. Вычисления можно делать как самостоятельно ручным способом, а можно использовать наш удобный калькулятор площади стен и периметра. Как вы сами понимаете второй метод наиболее предпочтительнее, практичнее и быстрее.
Было полезно? Поделитесь с друзьями!
Рубрики Строительные калькуляторы
Как посчитать площадь стен: делаем расчёты првильно
Начиная ремонт, первым делом нужно определить необходимое количество строительных материалов. Провести расчеты могут специалисты, которые будут выполнять работы. Но они часто делают вычисления с большой погрешностью в свою пользу. Рассмотрим, как самостоятельно посчитать площадь стен.
Провести расчеты могут специалисты, которые будут выполнять работы. Но они часто делают вычисления с большой погрешностью в свою пользу. Рассмотрим, как самостоятельно посчитать площадь стен.
Содержание
- 1 Инструменты для подсчета квадратных метров
- 2 Как рассчитать площадь прямоугольных стен
- 3 Как правильно рассчитать площадь стен со сложной поверхностью
- 3.1 Как посчитать квадратуру стен за вычетом проемов
- 3.2 Определение площади помещений неправильной формы
- 3.3 Как считать квадратные метры стен с круглыми элементами
- 3.4 Как рассчитать квадратные метры конструкций в виде треугольника
- 3.5 Объем помещения
- 4 Расчет площади стен дома на калькуляторе
- 5 Советы и рекомендации
Инструменты для подсчета квадратных метров
Для расчетов понадобятся:
- уровень строительный;
- рулетка с ограничителем;
- длинная линейка и угольник;
- карандаш и бумага;
- калькулятор.

Для нанесения размеров нарисуем схему комнат. Обозначим двери, окна, ниши, выступы. Результаты замеров нанесем на чертеж.
Как рассчитать площадь прямоугольных стен
Измеряем высоту (h), длину (a), ширину (b).
Площадь: S = P × h
Периметр: P = (a + b) × 2
Вдоль плинтуса измеряем длину и ширину помещений.
Высоту — по вертикальному углу.
Пример:
a = 5 м;
b = 4 м;
h = 3 м;
Р = (5 + 4) × 2 = 18 м;
S = 18 × 3 = 54 м².
Как правильно рассчитать площадь стен со сложной поверхностью
Не все помещения имеют строгую прямоугольную форму. В зданиях часто присутствуют замысловатые архитектурные элементы, усложняющие расчет.
Как посчитать квадратуру стен за вычетом проемов
При определении точного объема работ, вычтем размеры окон и дверей из общего количества квадратных метров стен комнаты. Для этого по краю рамы замеряем ширину и высоту окна, по краю коробки — габариты двери.
Перемножив длину и ширину проемов, получаем размер, который необходимо вычесть.
Аналогично действуем, если из подсчитываемой квадратуры комнаты нужно исключить печи, камины, радиаторы.
Пример:
В помещении имеется окно 2,5 м × 1,5 м и дверь 0,9 м × 2,1 м.
S окна равна 2,5 × 1,5 = 3,75 м².
S двери равна 0,9 × 2,1 = 1,89 м².
S стен за вычетом проемов составляет 54 − 3,75 − 1,89 = 48,36 м².
Определение площади помещений неправильной формы
Для определения периметра зданий любых конфигураций сложим длины всех стен, включая выступы и ниши.
Рисунок 1. Элемент с выступом.
Проводить измерения помещений неправильной формы можно, разбив поверхность на несколько простых фигур.
Если у вас комната с прямоугольным выступом, вы имеете две фигуры, квадратуру которых легко вычислить, затем сложить.
Если элемент содержит в себе полукруг, для расчета нужно разбить его на полукруг и прямоугольник.
Рисунок 2. Элемент с полукругом.
Как считать квадратные метры стен с круглыми элементами
Встречаются круглые и полукруглые жилые здания или строения с элементами окон или дверей в виде арки.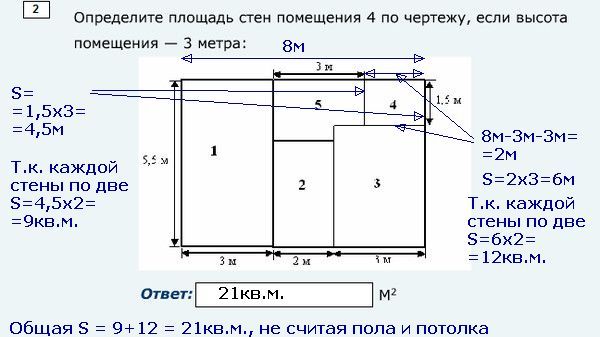
Их периметр можно определить, умножив диаметр на число π (Пи) = 3,14.
Квадратуру вертикальных поверхностей определяем, умножив полученное значение на высоту от пола до потолка.
S круга равна квадрату радиуса, умноженному на число π; полукруга — половине этой величины.
Если необходимо из квадратуры комнаты вычесть площадь круглых колонн или полукруглых выступающих элементов, при невозможности измерить диаметр или радиус, измеряем длину окружности (P) и применяем формулу: S = P² / 4π.
Как рассчитать квадратные метры конструкций в виде треугольника
В случае наличия комнаты с треугольными элементами, мы можем применить несколько формул, в зависимости от вида фигур:
Рисунок 3. Формулы определения площади треугольников.
Где a, b, c — длины сторон треугольника; p — периметр.
Объем помещения
Для определения объема необходимо высчитать площадь пола, и полученный показатель перемножить на высоту. V = S × h.
Расчет площади стен дома на калькуляторе
Существенно облегчат расчеты специальные программы, к которым относится строительный калькулятор в онлайн-версии.
Чтобы посмотреть, сколько квадратных метров составляют стены за вычетом проемов, достаточно выбрать геометрическую форму помещения и ввести показатели:
- ширину;
- длину;
- высоту;
- количество проемов;
- размеры окон и дверей.
Строительный калькулятор рассчитает количество отделочных материалов, необходимых для вашего ремонта.
Советы и рекомендации
Необходимо помнить, что геометрические параметры зданий редко могут быть идеальными. Поэтому для определения точных величин замеры лучше производить в нескольких местах, а затем выводить среднее арифметическое. Например, рассчитывая площадь комнаты по стенам, длину лучше измерять по потолку, плинтусу и в середине вертикальной плоскости. Высоту — в углах и середине стены по отвесу.
Чтобы вычислить периметр при наличии множества выступов и ниш разных форм, необходимо проложить вдоль всех элементов шнур, затем измерить его рулеткой.
Подсчитав точные параметры, можно идти в магазин за строительными материалами. Лучше показать схемы с нанесенными размерами продавцу-консультанту. Специалист поможет рассчитать расход материалов с учетом нахлеста, подбора рисунка обоев или потерь при резке плитки.
Лучше показать схемы с нанесенными размерами продавцу-консультанту. Специалист поможет рассчитать расход материалов с учетом нахлеста, подбора рисунка обоев или потерь при резке плитки.
Вычисление площади | SkillsYouNeed
Площадь — это мера того, сколько места внутри фигуры. Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может понадобиться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы посеять газон.
На этой странице собрана основная информация, которую вам необходимо знать, чтобы понимать и вычислять площади обычных фигур, включая квадраты и прямоугольники, треугольники и круги.
Расчет площади методом сетки
Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.
В этом примере внутри прямоугольника 10 квадратов сетки.
Чтобы найти значение площади с помощью метода сетки, нам нужно знать размер, который представляет квадрат сетки.
В этом примере используются сантиметры, но тот же метод применим для любой единицы длины или расстояния. Например, вы можете использовать дюймы, метры, мили, футы и т. д.
В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному «квадратному сантиметру».
Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.
Имеется 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.
В математике квадратные сантиметры сокращаются до см 2 . 2 означает «квадратный».
Каждый квадрат сетки равен 1 см 2 .
Площадь большого квадрата 16см 2 .
Подсчет квадратов на сетке для нахождения площади работает для всех фигур, если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.
В этом примере квадрат не вписывается точно в сетку.
Мы все еще можем вычислить площадь, считая квадраты сетки.
- Имеется 25 полных квадратов сетки (заштрихованы синим цветом).
- 10 половинных квадратов сетки (выделены желтым цветом) – 10 половинных квадратов соответствуют 5 полным квадратам.
- Также есть 1 четверть квадрата (заштриховано зеленым цветом) – (¼ или 0,25 целого квадрата).
- Сложите целые квадраты и дроби вместе: 25 + 5 + 0,25 = 30,25.
Следовательно, площадь этого квадрата равна 30,25 см 2 .
Вы также можете записать это как 30¼cm 2 .
Хотя использование сетки и подсчет квадратов внутри формы является очень простым способом изучения понятий площади, он менее полезен для нахождения точных площадей с более сложными формами, когда может быть много долей квадратов сетки, которые нужно сложить вместе.
Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.
Оставшаяся часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сетки.
Площади простых четырехугольников:
Квадраты, прямоугольники и параллелограммы
Простейшие (и наиболее часто используемые) вычисления площадей предназначены для квадратов и прямоугольников.
Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.
Площадь прямоугольника = высота × ширина
Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это само на себя, чтобы найти площадь. Это то же самое, что сказать длину 2 или длина в квадрате.
Хорошей практикой является проверка того, что фигура на самом деле является квадратом, путем измерения двух сторон. Например, стена комнаты может выглядеть как квадрат, но когда вы ее измерите, вы обнаружите, что на самом деле это прямоугольник.
Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.
Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.
Типовой план помещения не может состоять из простого прямоугольника или квадрата:
В этом и других подобных примерах хитрость заключается в том, чтобы разбить фигуру на несколько прямоугольников (или квадратов). Неважно, как вы разделите фигуру — любое из трех решений приведет к одному и тому же ответу.
Решение 1 и 2 требуют, чтобы вы сделали две фигуры и сложили их площади вместе, чтобы найти общую площадь.
Для решения 3 вы делаете большую фигуру (A) и вычитаете из нее меньшую фигуру (B), чтобы найти площадь.
Другая распространенная проблема заключается в том, чтобы найти область границы — фигура внутри другой фигуры.
В этом примере показан путь вокруг поля шириной 2 метра.
Опять же, в этом примере есть несколько способов определить площадь пути.
Вы можете рассматривать путь как четыре отдельных прямоугольника, вычислять их размеры, затем их площадь и, наконец, складывать площади вместе, чтобы получить общую сумму.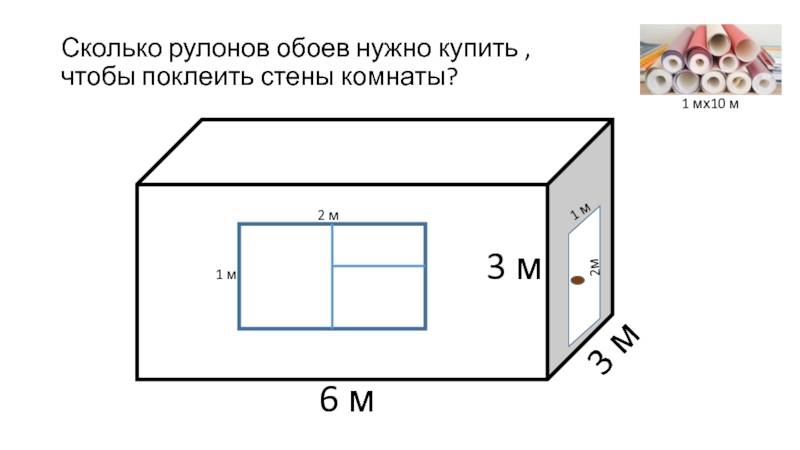
Более быстрым способом было бы определить площадь всей фигуры и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из целого, оставив площадь пути.
- Площадь всей фигуры 16 м × 10 м = 160 м 2 .
- Мы можем рассчитать размеры средней секции, потому что знаем, что путь по краю имеет ширину 2 м.
- Ширина всей фигуры 16 м, а ширина пути по всей фигуре 4 м (2 м слева от фигуры и 2 м справа). 16м — 4м = 12м
- То же самое можно сделать для высоты: 10 м — 2 м — 2 м = 6 м
- Итак, мы подсчитали, что средний прямоугольник имеет размеры 12 м × 6 м.
- Таким образом, площадь среднего прямоугольника равна: 12 м × 6 м = 72 м 2 .
- Наконец, мы отделяем площадь среднего прямоугольника от площади всей фигуры. 160 — 72 = 88м 2 .
Площадь пути 88 м 2 .
A Параллелограмм — это четырехсторонняя фигура с двумя парами сторон одинаковой длины — по определению прямоугольник — это разновидность параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехгранных фигурах с наклонными линиями, как показано здесь.
Однако большинство людей склонны думать о параллелограммах как о четырехгранных фигурах с наклонными линиями, как показано здесь.
Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что под высотой понимается не длина вертикальных (или не вертикальных) сторон, а расстояние между сторонами .
Из диаграммы видно, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.
Представьте воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.
Вычисление площади треугольников
Треугольник можно представить как половину квадрата или параллелограмма.
Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро вычислить его площадь, используя следующую формулу:
Площадь треугольника = (высота × ширина) ÷ 2.
Другими словами, вы можете вычислите площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите ответ на 2.
Высота треугольника измеряется как прямоугольная линия от нижней линии (основания) до «вершины» (верхней точки) треугольника.
Вот несколько примеров:
Площадь трех треугольников на диаграмме выше одинакова.
Каждый треугольник имеет ширину и высоту 3 см.
Площадь вычисляется:
(высота × ширина) ÷ 2
3 × 3 = 9
9 ÷ 2 = 4,5
Площадь каждого треугольника равна 4,5 см 2 .
В реальных ситуациях вы можете столкнуться с задачей, требующей нахождения площади треугольника, например:
Вы хотите покрасить фронтон сарая. Вы только хотите посетить отделочный магазин один раз, чтобы получить нужное количество краски. Вы знаете, что литр краски покроет 10м 2 стены. Сколько краски нужно, чтобы покрыть фронтон?
Вам нужно три измерения:
A — Общая высота до вершины крыши.
B — Высота вертикальных стен.
C — Ширина здания.
В этом примере размеры:
A — 12,4 м
B — 6,6 м
C — 11,6 м
Следующий этап требует дополнительных расчетов. Думайте о здании как о двух формах, прямоугольнике и треугольнике. По имеющимся у вас измерениям вы можете рассчитать дополнительные измерения, необходимые для определения площади конца фронтона.
Измерение D = 12,4 — 6,6
D = 5,8 м
Теперь вы можете разрабатывать площадь двух частей стены:
Площадь прямоугольной части стены: 6,6 × 11 = 76,56 м. 2
Площадь треугольной части стены: (5,8 × 11,6) ÷ 2 = 33,64 м 2
Сложите эти две площади вместе, чтобы найти общую площадь:
76,56 + 33,64 = 110,2 м 2
Как известно, один литр краски покрывает 10 м 2 стены, чтобы мы могли вычислить, сколько литров нам нужно купить:
110,2 ÷ 10 = 11,02 литра.
На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых банках, в результате получается чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но если мы не разбавим краску водой, этого будет недостаточно. Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкрашивания позже. И не забывайте, если вам нужно нанести более одного слоя краски, вы должны умножить количество краски на один слой на необходимое количество слоев!
У вас может возникнуть соблазн округлить до 11 литров, но если мы не разбавим краску водой, этого будет недостаточно. Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкрашивания позже. И не забывайте, если вам нужно нанести более одного слоя краски, вы должны умножить количество краски на один слой на необходимое количество слоев!
Площади кругов
Для вычисления площади круга необходимо знать его диаметр или радиус .
Диаметр окружности — это длина прямой линии от одной стороны окружности до другой, проходящей через центральную точку окружности. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)
Радиус окружности — это длина прямой линии от центральной точки окружности до ее края. Радиус равен половине диаметра. (радиус = диаметр ÷ 2)
Радиус равен половине диаметра. (радиус = диаметр ÷ 2)
Вы можете измерить диаметр или радиус в любой точке окружности – важно измерять с помощью прямой линии, которая проходит через (диаметр) или заканчивается (радиус) в центре окружности.
На практике при измерении окружностей часто бывает проще измерить диаметр, чем разделить его на 2, чтобы найти радиус.
Радиус нужен для вычисления площади круга, формула такова:
Площадь круга = πR 2 .
Это означает:
π = Pi — константа, равная 3,142.
R = радиус окружности.
R 2 (радиус в квадрате) означает радиус × радиус.
Следовательно, круг с радиусом 5 см имеет площадь:
3,142 × 5 × 5 = 78,55 см 2 .
Круг диаметром 3м имеет площадь:
Сначала вычисляем радиус (3м ÷ 2 = 1,5м)
Затем применяем формулу:
πR 2
3,142 × 1,5 × 1,5 = 7,0695.
Площадь круга диаметром 3 м равна 7,0695 м 2 .
Заключительный пример
Этот пример использует большую часть содержимого этой страницы для решения простых задач с площадями.
Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (регистрационный номер: 376599).
Этот пример включает в себя нахождение площади фасада дома, деревянной решетчатой части, исключая дверь и окна. Вам нужны следующие мерки:
| А – 9,7 м | В – 7,6 м |
| С – 8,8 м | Г – 4,5 м |
| В – 2,3 м | В – 2,7 м |
| Г – 1,2 м | В – 1,0 м |
Примечания:
- Все измерения являются приблизительными.
- О бордюре вокруг дома можно не беспокоиться – он не учитывался при измерениях.
- Предполагается, что все прямоугольные окна имеют одинаковый размер.

- Размер круглого окна — это диаметр окна.
- Размеры двери включают ступени.
Какова площадь деревянной решетчатой части дома?
Вычисления и ответы ниже:
Ответы на приведенный выше пример
Сначала вычислите площадь основной формы дома – прямоугольника и треугольника, составляющих фигуру.
Основной прямоугольник (В × С) 7,6 × 8,8 = 66,88м 2 .
Высота треугольника (A – B) 9,7 – 7,6 = 2,1.
Следовательно, площадь треугольника равна (2,1 × C) ÷ 2,
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м 2 .
Суммарная полная площадь фасада дома равна сумме площадей прямоугольника и треугольника:
66,88 + 9,24 = 76,12 м 2 .
Затем определите площади окон и дверей, чтобы их можно было вычесть из общей площади.
Площадь двери и ступеней составляет (D × E) 4,5 × 2,3 = 10,35 м 2 .
Площадь одного прямоугольного окна составляет (G × F) 1,2 × 2,7 = 3,24 м 2 .
Пять прямоугольных окон. Умножьте площадь одного окна на 5.
3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).
Круглое окно имеет диаметр 1 м, поэтому его радиус равен 0,5 м.
Используя πR 2 , определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855 м 2 .
Затем добавьте площади дверей и окон.
(площадь дверей) 10,35 + (площадь прямоугольных окон) 16,2 + (площадь круглых окон) 0,7855 = 27,3355
Наконец, вычтите общую площадь окон и дверей из полной площади.
76,12 – 27,3355 = 48,7845
Площадь деревянного реечного фасада дома, а ответ на задачу: 48,7845м 2 .
Вы можете округлить ответ до 48,8 м 2 или 49 м 2 .
См. нашу страницу по Оценка, приближение и округление .
Дальнейшее чтение из книги «Навыки, которые вам нужны»
Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»
В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства фигур, линий и твердых тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Как определить площадь стен, пола или покраски?
– Строительный мат
При измерении площади, которую вы хотите покрыть, например, стены, на которой вы хотите поместить стены из растений, или площади пола, которую вам нужно выложить плиткой, или даже фартука, вам придется рассчитать количество квадратных метров. чтобы выяснить, сколько материала вам нужно.
Как считать квадратные метры?
В общем случае пространство, для которого вы будете рассчитывать квадратные метры, будет плоской квадратной поверхностью, если оно не квадратное, вам нужно будет попытаться разбить общую площадь на разные квадратные участки и вычислить каждый общий квадратный метр на складывая каждый из рассчитанных блоков квадратных метров вместе, чтобы измерить площадь, вам обязательно понадобится рулетка под рукой.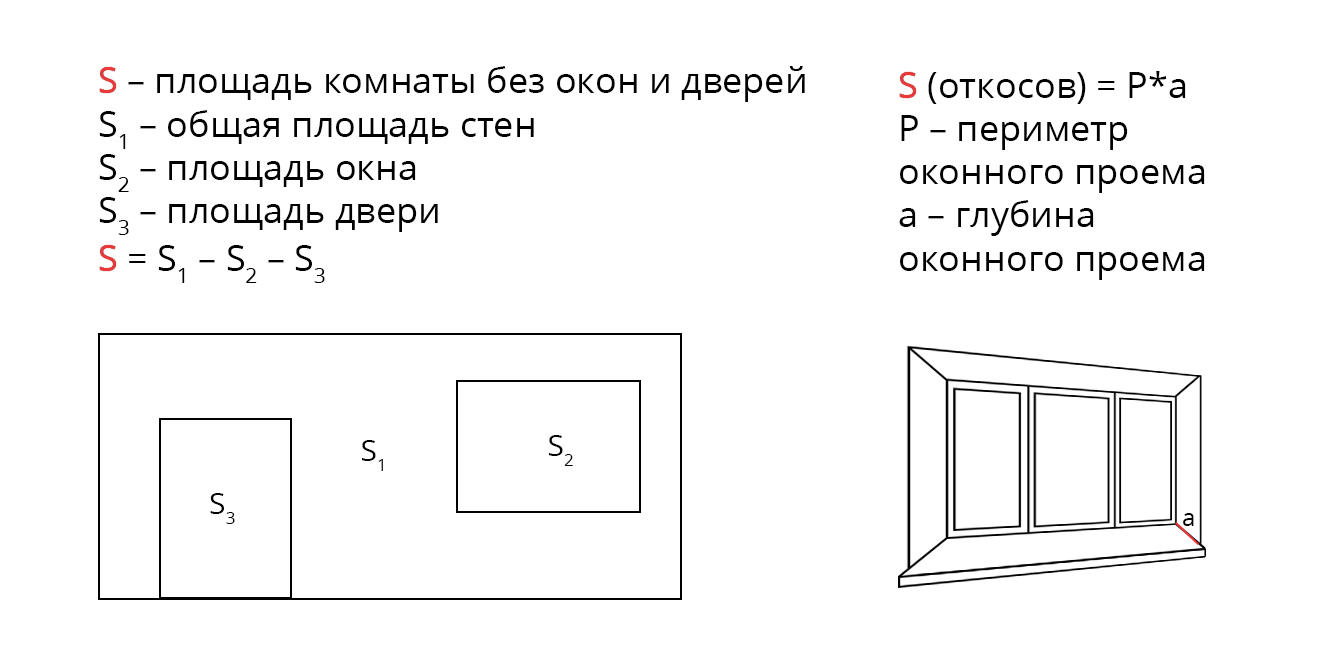
Чтобы рассчитать квадратный метр, вам нужно будет использовать рулетку и узнать длину и ширину комнаты.
По какой формуле рассчитать квадратные метры?
Формула довольно проста: длина умножается на ширину, чтобы получить площадь комнаты в квадратных метрах.
Что такое 1 кв.м.?
это аббревиатура, используемая для обозначения 1 квадратного метра, поэтому 1 квадратный метр равен 1 квадратному метру.
Какая разница между метрами и метрами?
Эти две единицы измерения одинаковы, метры используются в американском английском, тогда как метры используются в британском английском. То же самое касается единиц площади, таких как квадратные метры в квадрате и квадратные метры.
Есть ли разница между квадратными метрами и квадратными метрами?
Да, есть большая разница между квадратных метров и s квадратных метров. 90 040 квадратных метров рассчитывается путем умножения длины на ширину, тогда как метры в квадрате имеют одинаковую длину и ширину.
- 1 метр в квадрате равен 1 метру длины и 1 метру ширины, следовательно, равен 1 квадратному метру.
- 3 метра в квадрате — это 3 метра длины, умноженные на 3 метра ширины, что составляет 9 квадратных метров.
3 квадратных метра могут быть 1 метр длины, умноженный на 3 метра ширины, что составляет 3 квадратных метра, это очень запутанно, но вы можете видеть, что это не то же самое, что 3 метра в квадрате.
Итак, когда кто-то говорит « квадратных метров «, а не « квадратных метров «, мы всегда будем перепроверять, означают ли они квадратный метр или метры в квадрате.
Как мне преобразовать квадратные метры в квадратные футы?
давайте обсудим различные метрические преобразования, 1 квадратный метр эквивалентен 10,764 квадратных фута. , то есть, чтобы преобразовать квадратный метр в квадратный фут, умножьте значение площади на 10,764. Например, 3 кв.
Как перевести квадратные метры в квадратные ярды?
1 квадратный метр равен 1,19599 квадратных ярдов, поэтому, чтобы преобразовать квадратный метр в квадратные футы, умножьте значение площади на 1,19599.


