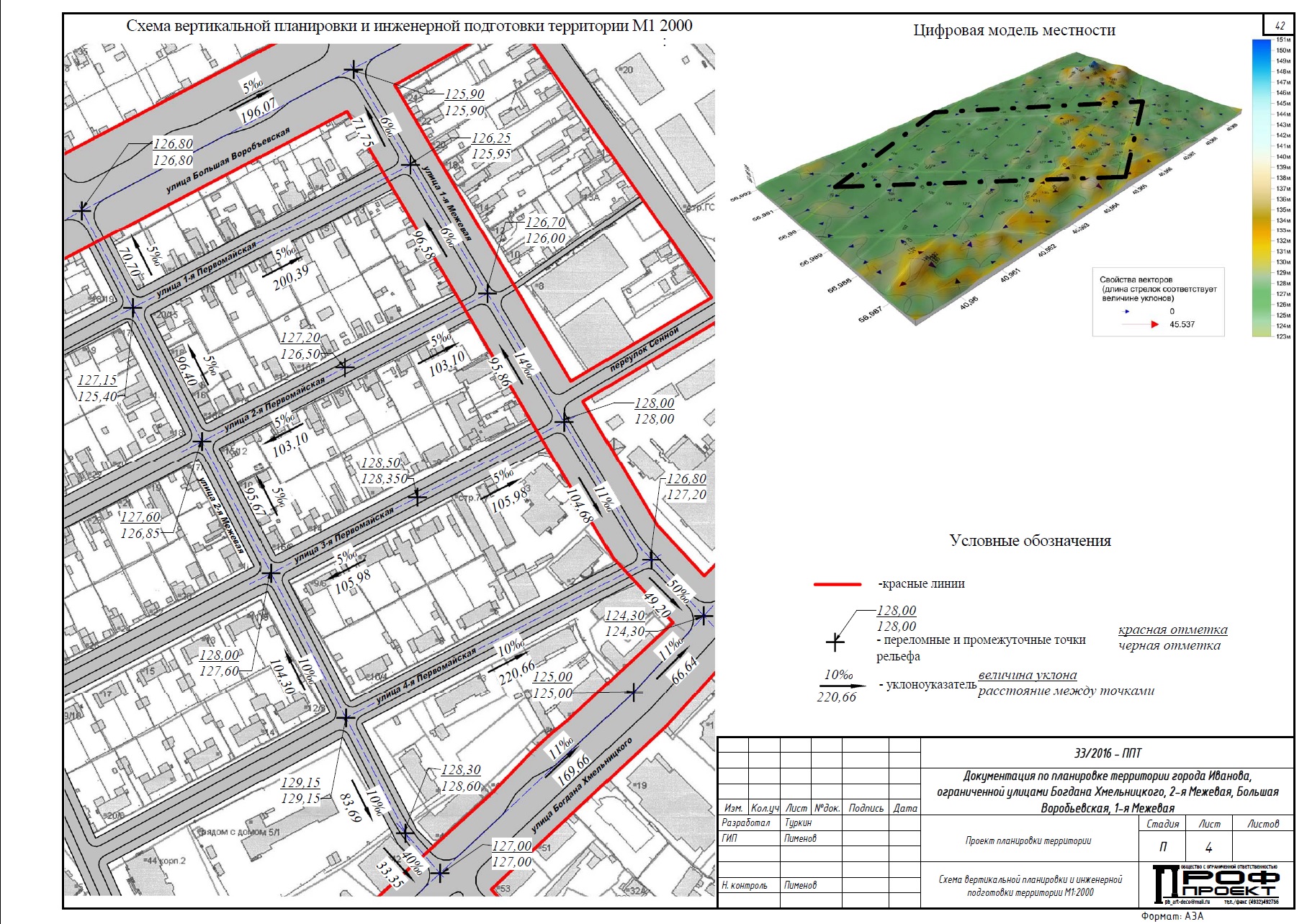
6. Проектирование вертикальной планировки

Цель работы:
освоить
геодезические расчеты при проектировании
наклонной площадки с соблюдением
нулевого баланса земляных работ.

6.1. Общие понятия

Проект вертикальной
планировки является составной частью
генерального плана строительства и
имеет целью преобразование естественных
форм рельефа в рельеф, удобный для
эксплуатации инженерных сооружений.
На его основе разрабатывается проект
производства земляных работ.

Графическим
документом вертикальной планировки
является картограмм земляных работ, на
которой указываются отметки земли,
проектные отметки, рабочие отметки,
характеризующие объемы насыпей и глубины
выемок в точках площадки, значения
объемов насыпей и выемок, как по всей
площадке, так и по ее отдельным частям.

Основой составления
проекта вертикальной планировки служат
топографические планы масштабов 1:500 –
1:1000 с высотой сечения рельефа 0. 5 – 1.0
метра, составленные по результатам
тахеометрической съемки или нивелирования
строительной площадки по квадратам.

Рельеф строительного
участка может быть спланирован
горизонтальной или наклонной плоскостью
при условии нулевого баланса земляных
работ или по заданной отметке какой-либо
точки площадки. Баланс земляных работ
определяется формулой

V
= V_Н
+ V_В
,

(6.1)

где V_Н
– объем насыпи (со знаком плюс) в пределах
площадки),

V_В
– объем выемки (со знаком минус).

Вертикальная
планировка при условии V=0
ведется на незастроенной территории,
по заданной отметке – на застроенной,
когда строительный участок по высоте
необходимо увязать с существующей
планировкой.

При проектировании
наклонной плоскости общий уклон площадки
и его направление назначают в соответствии
с техническими условиями на проектирование
данного типа сооружения, задачами
благоустройства, рельефом местности.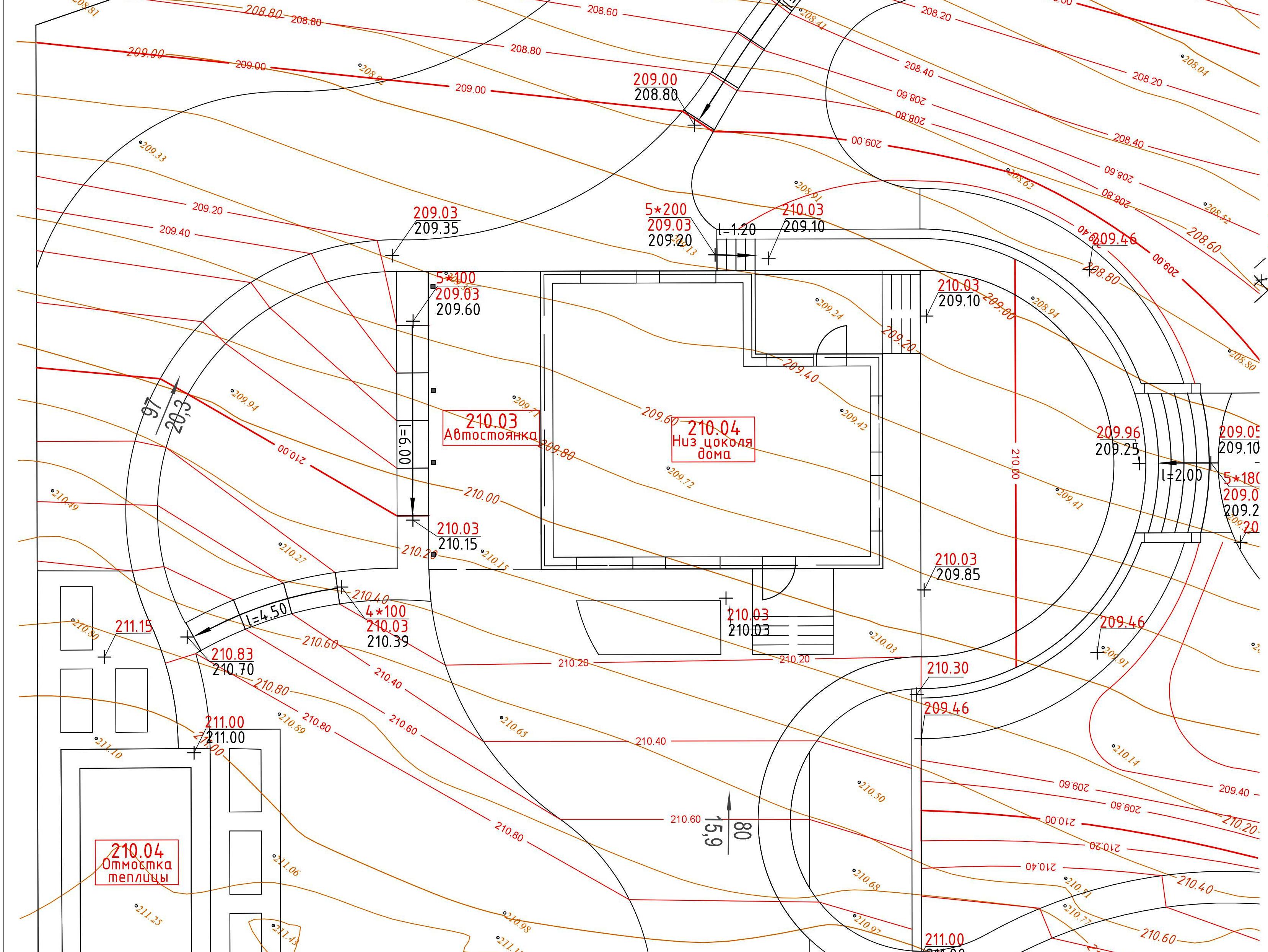

Картограмма
земляных работ, как правило, составляется
по регулярной сетке квадратов с
вычислением объемов земляных работ по
рабочим отметкам вершин квадратов. Для
повышения точности вычисления объемов
земляных работ каждый квадрат разбивают
на треугольники направленными
диагоналями,
являющиеся основаниями элементарных
земляных тел. Объемы этих тел вычисляют
по формуле треугольной призмы

v
= ()s
/ 3,

(6.2)

где s
– площадь треугольника,

hi
– рабочие отметки вершин треугольника.

Объемы
земляных работ в каждом квадрате будут
равны суммам объемов элементарных
треугольных призм.

Вычисление
объемов земляных работ по треугольным
призмам или с применением микрокалькуляторов
является весьма трудоемким. Такая задача
может быть решена достаточно быстро и
качественно на ЭВМ.

Программа
«Вертикальная планировка топографической
поверхности – vpltp»
приведена в
.

Программа
может быть использована студентами 1
курса при выполнении расчетно-графической
работы на практических занятиях и на
учебной геодезической практике.

6.2. Методика проектирования

На
топографический план, составленный по
результатам тахеометрической съемки,
в пределах границ планируемого участка
наносится сетка квадратов с заданной
стороной d
, см. пример на рис. 6.1. Ориентирование
сетки квадратов произвольное. Сторона
d
на плане обычно принимается равной 2
см. На рис. 6.1 построена сетка квадратов
со стороной 3 см, что соответствует на
местности 30 м.

Рис.
6.1. Топографический план

Отметки вершин
квадратов определяют по горизонталям
плана графической интерполяцией и
выписывают на расчетную схему (рис.
6.2).

На
расчетной схеме проводят горизонтали,
подписывают оси координат: ось Х —
вертикальная линия, ось У – горизонтальная
линия (система координат площадки).

Если
топографический план составлен по
результатам нивелирования поверхности
по квадратам, то на нем уже имеется сетка
квадратов и отметки вершин квадратов,
выписанные из журнала до 0. 01 м.

Рис. 6.2. Расчетная
схема вертикальной планировки
топографической поверхности

длина стороны
квадрата d
= 30 м.; число квадратов по осям координат:
nx=4,

ny
=3; отметка исходной точки H₀
=66.4 м; координаты исходной точки в системе
координат площадки: Х₀
=0, Y₀
=0; уклоны по осям координат площадки
i
_x
= — 0.012, i
_y
= — 0.004

Сообразуясь с
формами рельефа, в каждом квадрате
проводят диагональ. Диагонали выбирают
так, чтобы в каждом треугольнике был
однообразный склон. Возможны два
положения диагонали в квадрате i
j
(номер квадрата определяется номером
левой нижней вершины квадрата) – признаки
t
_ij
=0 и t
_ij
=1 (рис.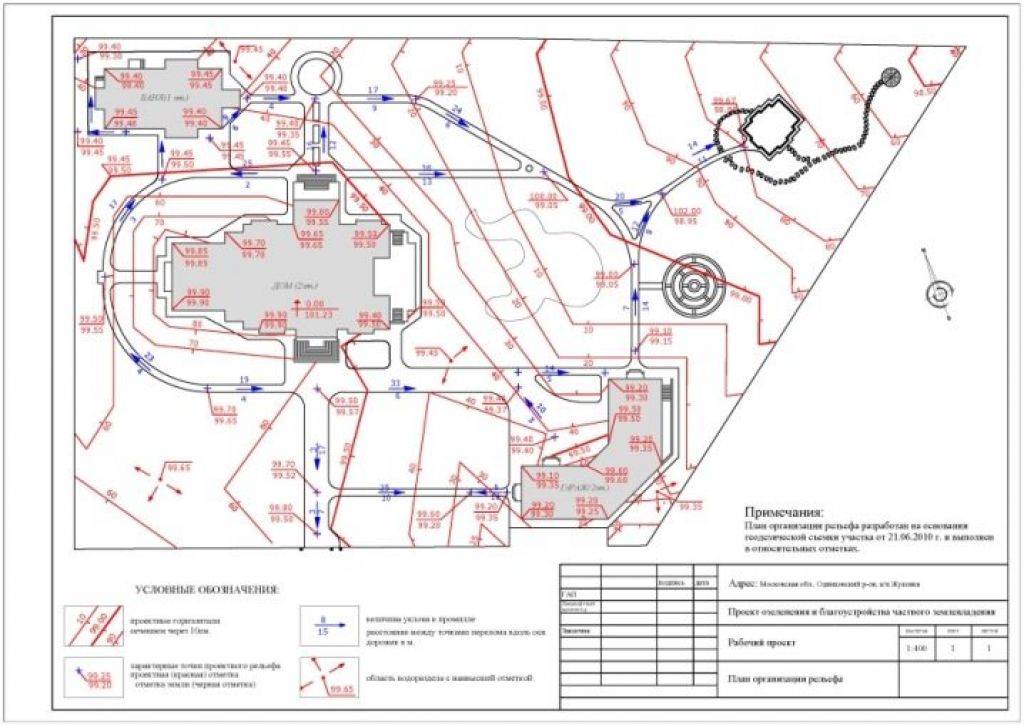 6.3).

Если
в квадрате однообразный склон, то
диагонали можно выбрать произвольно:
0 или 1. Можно придерживаться принципа:
диагонали проводятся перпендикулярно
горизонталям, примерно, (рис. 6.2).

Рис. 6.3. Схема
разбивки квадратов на треугольники
направленными диагоналями

t
_i
j
=0 – диагональ не проходит через вершину
i
j

t
_i
j
=1 – диагональ проходит через вершину
i
j

Диагонали
показывают на расчетной схеме и выписывают
их признаки t
_ij
.

В
соответствии с техническими условиями
на проектирование, задачами благоустройства,
рельефом местности, характеризуемом
горизонталями, назначают общий уклон
i₀
площадки и его направление r
относительно оси Х в системе координат
площадки.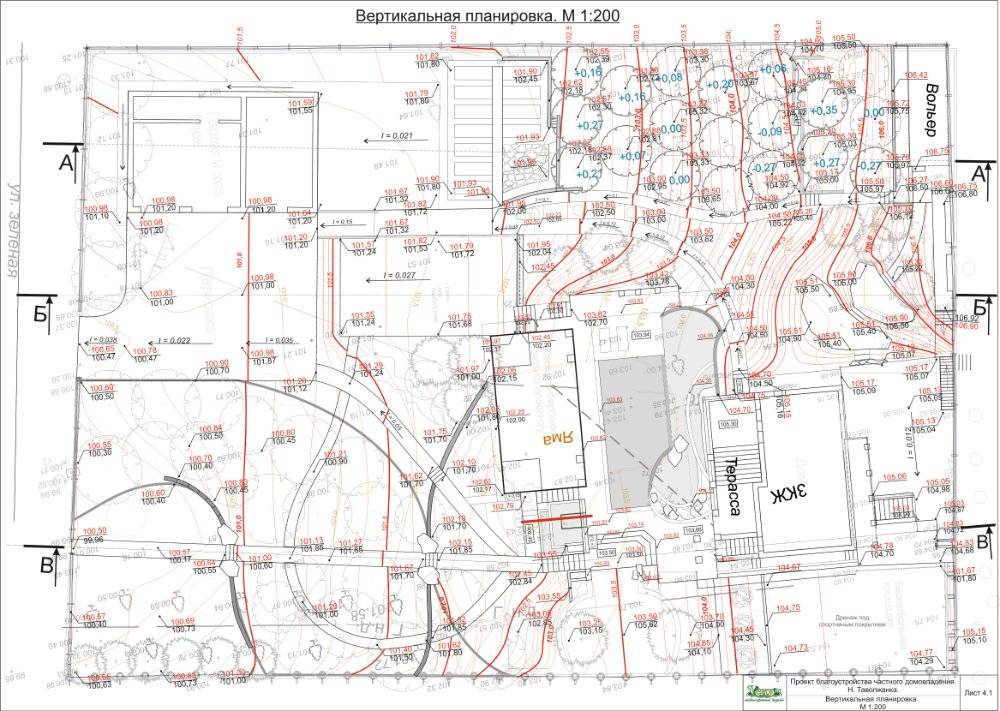

Направление
уклона выбирают согласно рельефу. Так
на рис. 6.2 направление уклона r
=20⁰
— направление дна лощины.

Величину
уклона i₀
назначают из условия: 0.003 
i₀

0.013 (условие вертикальной планировки
городских территорий). Для выбора i₀
можно определить максимальный уклон
i
_max
площадки. Так на рис. 6.1 уклон по дну
лощины между точками с отметками 65.3 и
61.5, расстояние между которыми 110 метров
по плану, равен

i
_max
= ( 61.5 – 65.3) / 110 = — 0.036.

Уклон
превышает максимальный по техническим
условиям. Следовательно, можно назначить
i₀
= 0.013. Если i
_max
площадки лежит в диапазоне технических
условий, то можно назначать i₀
= i
_max
площадки.

Возможны
другие технические условия. Выбор уклона
и его направление – задача
архитектурно-планировочного решения.
Но если уклон задан, то дальнейший расчет
геодезический.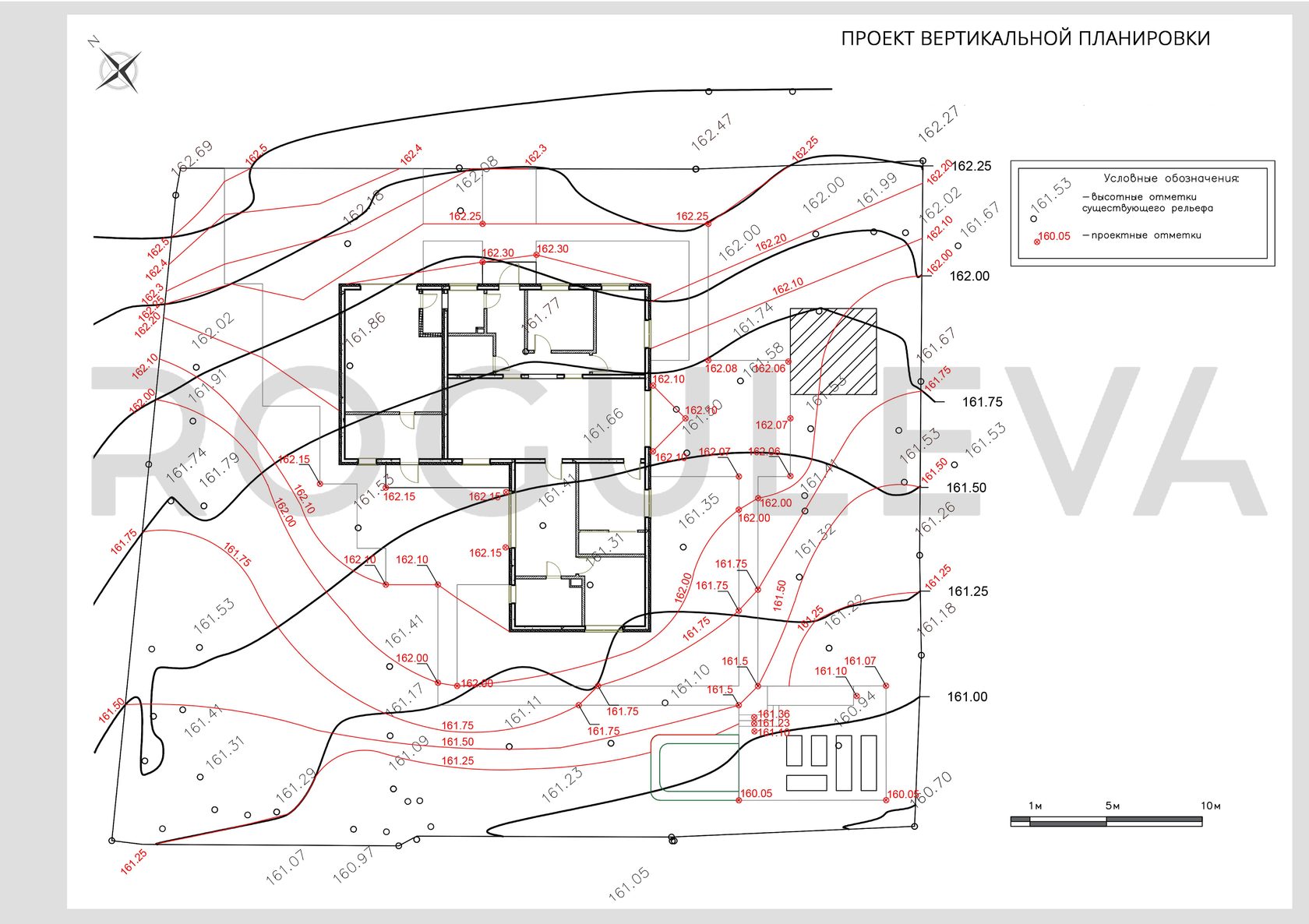

Вычисляют
уклоны i
_x
и i
_y
по осям координат площадки:

i _x
= i₀

cos r , i _y
= i₀

sin r . (6.3)

Округляют до 0.001
и выписывают на расчетную схему (рис.
6.2).

На
строительных чертежах уклоны обозначают
стрелками, над которыми выписывают
модули уклонов. На ЭВМ проектные отметки
вычисляются по оси У слева – направо
и по оси Х снизу – вверх. Поэтому на
рис. 6.2 уклоны для ЭВМ запишем как i_x
= — 0.012, i
_y
= — 0.004.

Выписывают
проектную отметку Н₀
исходной точки площадки, если
проектирование ведется по заданной
отметке, или произвольно назначают
отметку Н₀
любой точки площадки, если проектирование
ведется при условии нулевого баланса
земляных работ. Определяют координаты
Х₀
и У₀
точки с отметкой Н₀
в системе координат площадки. Так на
рис. 6.2 при условии V
= 0 приняли: Н₀
= 66.4, Х₀
= 0, У₀
= 0. На схему выписывается число квадратов
по осям координат: nx
и ny.

В
вычислительном центре в ЭВМ непосредственно
с чертежа (рис. 6.2) вводят исходную
информацию строго в соответствии с
указаниями, появляющимися на экране.
На дисплей ЭВМ выводятся отметки земли
вершин квадратов (это необходимо для
контроля правильности ввода их в память
ЭВМ), проектные и рабочие отметки, объемы
земляных работ по каждому квадрату и
суммарные объемы. А также для контроля
проектная отметка исходной точки, длина
стороны квадрата, число квадратов по
осям координат и проектные уклоны.

При
проектировании по нулевому балансу
земляных работ вывод на дисплей
результатов вычислений производится
при условии

V

10 м³.
(6.4)

Если условие (6.4)
не выполняется, то уточняется отметка
Н₀
по формуле

Н₀
= Н₀
— V
/ F,
(6. 5)

где
F
– площадь всего участка в м²
. Повторно вычисляются объемы земляных
работ и снова производится проверка
условия (6.4), (итерационный процесс).

Результаты
вычислений – проектные и рабочие
отметки, объемы земляных работ по каждому
квадрату и суммарные объемы, баланс
земляных работ — выписываются на
картограмму земляных работ (рис. 6.4).
Положение линии нулевых работ (обозначается
пунктирной линией) определяют на
картограмме графической интерполяцией
по сторонам квадратов. Правильность
вычислений проверить по проектным
уклонам: разность проектных отметок
двух смежных вершин должна равняться
произведению уклона на длину стороны
квадрата (с учетом знака уклона). Основная
ошибка: неправильный ввод знаков уклонов.
В этом случае вычисления на ЭВМ повторить.

Вертикальная планировка участка и строительной площадки

Садовый участок вокруг дома может быть ровным или наклонным. Независимо от рельефа в процессе планировки сада обязательно потребуется проект вертикальной планировки участка.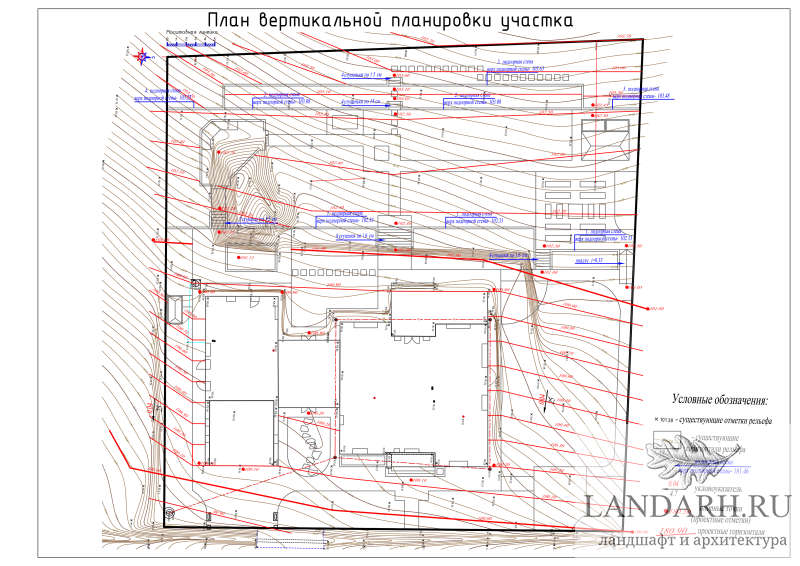

Под вертикальной планировкой подразумевается проведение инженерных работ по искусственному изменению, преобразованию и улучшению рельефа местности. Вертикальная планировка площади является одной из наиболее важных процедур в процессе благоустройства и инженерной подготовки территорий.

Занимаясь организацией рельефа участка, необходимо стараться свести к минимуму объём проводимых работ, при этом сохранив растительный грунт и выполнив некоторые требования:

1. Создавая площадки, требуется учитывать их деление на функциональные зоны, а также организацию отвода ливневых и паводковых вод с земельного участка.
2. Снижение уровня грунтовых вод.
3. Отвод ливневых вод не должен осуществляться через зону жилого здания.
4. Полная изоляция от остальных стоков отвода ливневых вод со двора.

На земельном участке, обладающем перепадами в уровне расположения отдельных территорий относительно поверхности земли, требуется проведение тщательной вертикальной планировки участка. Одним из самых простых элементов вертикальной планировки являются откосы, которые представляют собой переход с одного участка на другой при разнице их уровней.

На этом видео можете посмотреть на пример вертикальной планировки от профессиональных архитекторов.

Как правило, проект вертикальной планировки участка осуществляется в следующем порядке:

1. Планировка аллей, парковых дорожек, площадок различного назначения – то есть, планировочных элементов территории, требующих внимательного соблюдения возможных уклонов поверхности.
2. Изготовление проектов для зелёных насаждений – планировочных элементов, допускающих разнообразные уклоны поверхности.

Вернуться к оглавлению

Содержание материала

• 1 Этапы, входящие в проектирование вертикальной планировки участка
• 2 Методы вертикальной планировки

Этапы, входящие в проектирование вертикальной планировки участка

1. Создание детальной схемы планировки территории, а также построение её высотного каркаса с дальнейшим определением общего высотного решения участка в соответствии с проектными отметками и уклонами поверхности, обеспечивающими организацию стока талых и поверхностных вод.
2. Создание подробного проекта вертикального решения участка с помощью наведения новых горизонталей и проектирования нового рельефа местности.
3. Рабочая стадия, в которую входят разработка детальной картограммы земляных работ, с точным расчётом объёмов грунта.

Грамотно проведённый план может значительно улучшить вид земельного участка, а также его гигиеническое состояние, избавив территорию от скоплений грязи и воды.

По словам ландшафтных дизайнеров, оптимальным рельефом земельного участка считается тот, который ровный или наклонён к югу или востоку. Остальных направлений, в особенности, в северную сторону, следует избегать.

Пример вертикальной планировки участкаВернуться к оглавлению

Методы вертикальной планировки

Очень часто владельцы неровных и наклонных участков сталкиваются с тем, что на подобной местности просто невозможно воплотить в жизнь многие идеи по оформлению ландшафта. По этой причине необходимо обратиться за помощью к специалистам, для которых расчёт вертикальной планировки для извлечения пользы из самых скудных участков не представляет никакой сложности.

Если ландшафт сада достаточно ровный, то здесь можно расположить жилое здание, садовые постройки, различные зелёные насаждения. Как правило, рядом со стенами возводят уклоны небольших размеров, предназначенные для отвода грунтовых вод к границам участка или основным дорожкам. Уклон создают при помощи насыпи грунта в необходимых местах участка, а сами дорожки делают из твёрдых материалов. Кроме этого, с обеих сторон делают дренаж качественного отвода ливневой воды к дорожному кювету. Эти работы также можно проводить при многих других видах планировки участка.

Небольшие уклоны, сделанные при планировке садового участка

Проект вертикальной планировки территории с уклоном в южную сторону позволяет получить достаточно насыщенную растительность, так как деревья и кустарники на таком склоне растут просто замечательно. Жилой дом в этом случае рекомендуется располагать на самой верхней точке участке, как можно ближе к восточной границе. Хозяйственные постройки, в свою очередь, желательно размещать внизу площадки.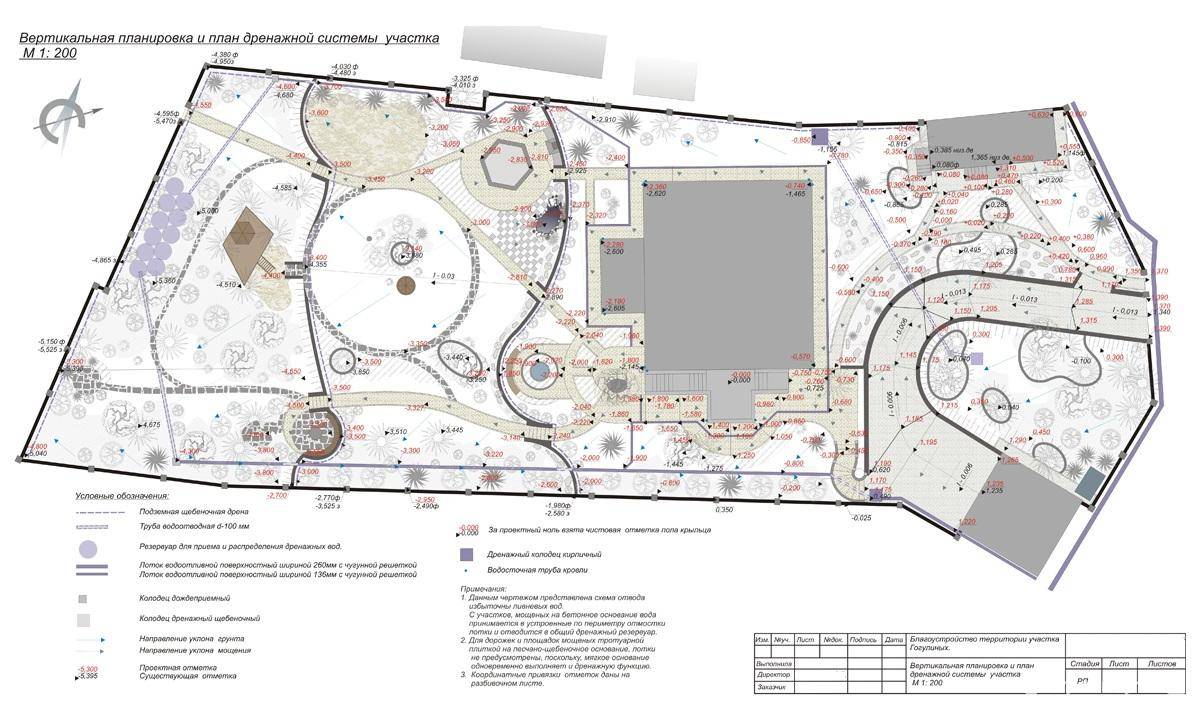

Вид вертикальной планировки, при которой жилой дом расположен в самом верху участка

Если участок обладает наклоном в западную и восточную стороны, строения необходимо располагать у северной границы таким образом, чтобы они не мешали растительности. Схема вертикальной планировки в этом случае подразумевает расположение перед домом. Высокие деревья рекомендуется высаживать за садовыми постройками, чтобы тень от строений не мешала им развиваться.

Немного сложнее проводить земляные работы, если участок обладает уклоном более 20° (независимо от того, в какую сторону идёт уклон). Уклон довольно-таки крутой, поэтому во время дождей нередко образуется большое количество воды, смывающей всё на своем пути. В этой ситуации потребуется качественная вертикальная планировка с дренажной системой.

Пример вертикальной планировки территории с наклоном более 20 градусов

Горизонтальные площадки необходимо формировать дополнительным грунтом, при этом оформляя с боков при помощи плитки, натурального камня и кирпичной кладки.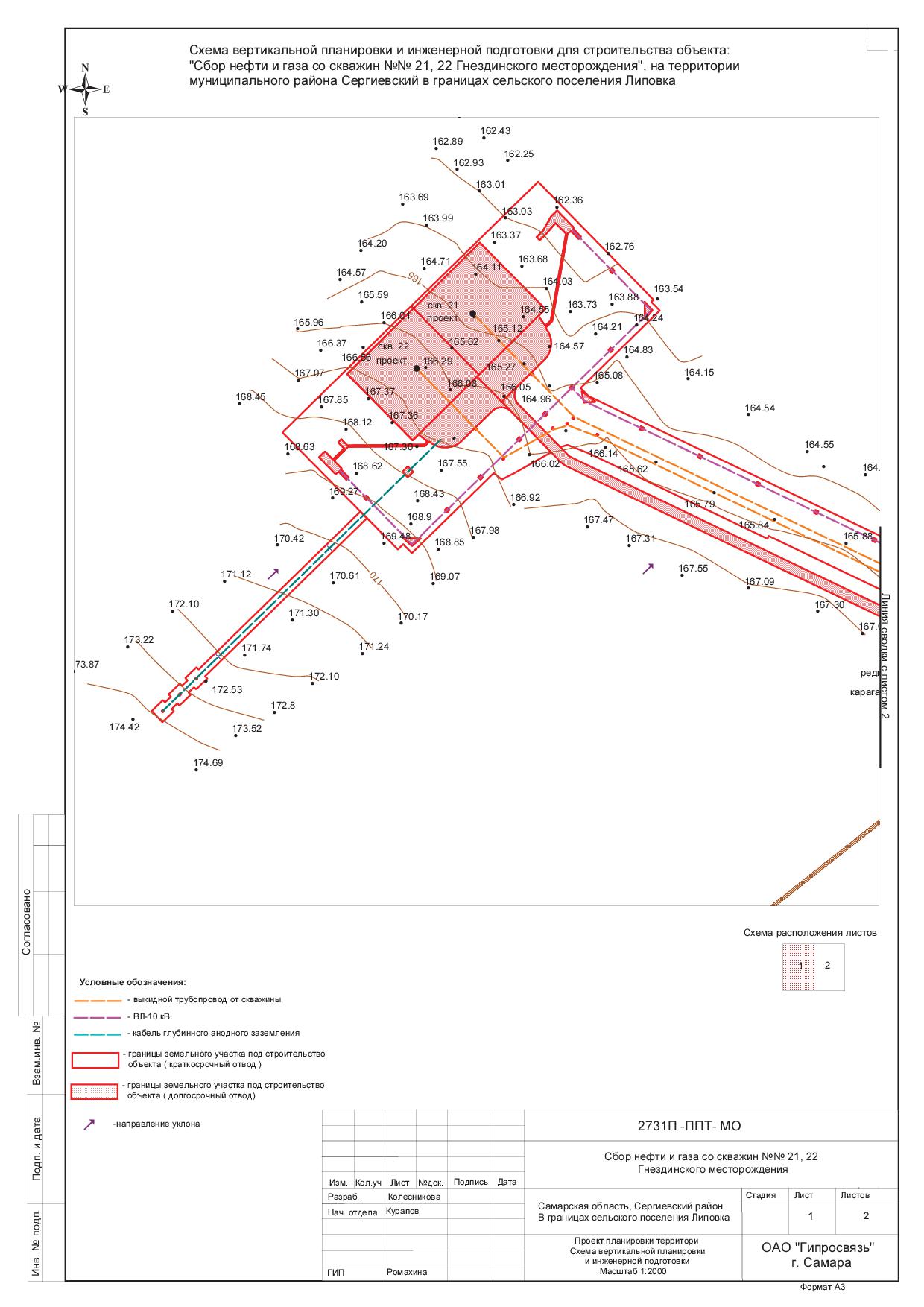 Высокие откосы укрепляют деревянными колышками и бетонным раствором. Оформляя откосы камнем, его необходимо плотно укрепить в специально подготовленных углублениях. Снизу, как правило, находится крупный булыжник, а сверху – мелкая галька.

Руководство по проектированию дорог MnDOT

Перейти к Руководству по проектированию объектов

MnDOT переходит от Руководства по проектированию дорог (RDM) к документу-преемнику, Руководству по проектированию объектов (FDG). Во время этого перехода обе публикации будут активны и онлайн. Вы можете перемещаться между публикациями с помощью синей кнопки выше.

По мере публикации новых разделов FDG соответствующие материалы RDM будут удаляться, а ссылки на новые материалы вставляться вместо них. Если вы еще не включены в список электронной рассылки этих документов, зарегистрируйтесь
здесь
будет предупреждать вас о новых обновлениях по мере их появления.

Приносим извинения за неудобства. Спасибо, что были с нами, пока мы обновляем наше руководство по дизайну дорог и улиц.

Текущие главы

Последние обновления

Полное руководство

Исторические версии

Метрическая система (Снято с производства)

Просмотр страницы 1 из 1 Показывать 102050100ВСЕ Записей на странице

Глава Название Дата Пересылка 00 Обложка, содержание и т. д. 28.11.2018 18-01 01 Дизайн Функции и обязанности 28.11.2018 18-01 02 Стандарты проектирования автомобильных дорог 22.02.2023 23-02 03 Выравнивание и вираж 01. 02.2021 21-01 04 Поперечные сечения 07.03.2023 23-03 05 Перекрестки на уровне земли 07.12.2022 22-03 06 Развязки и разделения уровней 07. 12.2022 22-03 07 Дизайн дорожного покрытия 07.03.2022 22-02 08 Проектирование дренажа и защита от эрозии 01.06.2021 21-02 09 Мосты и другие сооружения 09. 04.2008 08-01 10 Устройства управления дорожным движением и дорожные барьеры 07.03.2023 23-03 11 Специальное исполнение 06.01.2022 22-01 12 Руководство по проектированию современных кольцевых развязок 10. 11.2021 21-03 ВСЕ Полный RDM (с возможностью поиска в формате pdf) 07.03.2023 23-03 Показывать 102050100Все Записей на странице

Выберите главу

~Выберите главу~00 — Титульный лист, содержание и т. д.01 — Функции и обязанности при проектировании02 — Стандарты проектирования автомобильных дорог03 — Выравнивание и вираж04 — Поперечные сечения05 — Перекрестки на уровне земли06 — Развязки и разделение уровней07 — Проектирование дорожного покрытия08 — Дренаж Дизайн и защита от эрозии09- Мосты и другие сооружения10 — Устройства управления дорожным движением и дорожные ограждения11 — Специальные конструкции12 — Рекомендации по проектированию современных кольцевых развязокВСЕ — Полный RDM (pdf с возможностью поиска)

• Дизайн сцены
• Образец плана метро
• Стандартные пластины
• Стандартные планы
• Стандартные технические условия для строительства
• Технические меморандумы
• Дизайн безопасности на дорогах

групп макетов | Изучите PlayCanvas

Компонент группы макетов используется для автоматической установки положения и размера дочерних элементов. Компонент группы макетов можно использовать для выравнивания
дочерние элементы в вертикальные или горизонтальные столбцы или сетку. Компонент группы макетов применяет правила макета ко всем своим непосредственным дочерним элементам.
может переопределить правила группы макетов для одного дочернего элемента с помощью дочернего компонента макета.

Компонент группы макетов можно использовать для создания общих макетов, например сетки, вертикального столбца фиксированной ширины или горизонтального ряда.

Создание группы макетов

Добавьте группу макетов, добавив компонент LayoutGroup к существующему элементу.

Свойства группы макетов

Ориентация

Установите для параметра Orientation значение Horizontal, чтобы упорядочить макет слева направо или справа налево. Или по вертикали, чтобы организовать макет
сверху вниз или снизу вверх

Реверс

Свойства ReverseX и ReverseY используются для задания направления построения группы макетов. По умолчанию — слева направо и снизу вверх.

Выравнивание

Выравнивание используется для выравнивания дочерних элементов по краям группы макетов. [0,0] выравнивается по левому нижнему краю, [1,1]
выравнивается по правому верхнему углу.

Прокладка

Padding добавляет пространство внутри группы макетов перед размещением каких-либо дочерних элементов.

Интервал

Интервал определяет промежуток между каждым дочерним элементом.

Фитинг

Свойства Подгонка по ширине и Подгонка по высоте определяют, как ширина или высота дочернего элемента будет регулироваться группой макетов.

Значение None не будет применяться.

Значение Stretch будет растягивать дочерние элементы, чтобы заполнить ширину или высоту контейнера, используя следующую процедуру:

• Суммируйте значения fitWidthProportion/fitHeightProportion каждого дочернего элемента и нормализуйте так, чтобы сумма всех значений равнялась 1.
• Применить естественную ширину/высоту для каждого дочернего элемента.
• Если в контейнере осталось место, распределите его между каждым дочерним элементом на основе нормализованного значения fitWidthProportion/fitHeightProportion
  значения, но не превышайте maxWidth/maxHeight каждого дочернего элемента.

Значение Shrink уменьшит дочерние элементы, чтобы они соответствовали контейнеру, используя следующую процедуру:

• Суммируйте значения fitWidthProportion/fitHeightProportion каждого дочернего элемента и нормализуйте так, чтобы сумма всех значений равнялась 1.
• Применить естественную ширину/высоту для каждого дочернего элемента.
• Если новая общая ширина/высота всех дочерних элементов превышает доступное пространство контейнера, уменьшите ширину/высоту каждого дочернего элемента
  пропорционально на основе нормализованных значений fitWidthProportion/fitHeightProportion, но не превышать minWidth/minHeight каждого
  ребенок.

Значение Оба будут применять как Растягивание , так и Сжатие .

Обертка

Свойство переноса приводит к тому, что дочерние элементы, выходящие за пределы ширины (для вертикальных групп) или высоты (для горизонтальных групп), перемещаются в новую строку
или колонка. Используя свойство wrap, вы можете создавать макеты на основе сетки.

Макет Дети

Группа макетов применяет свои правила ко всем своим непосредственным дочерним элементам. Если вы хотите переопределить эти правила для конкретного ребенка, вы можете сделать это,
добавление компонента LayoutChild к этому дочернему элементу.

В этом примере горизонтальная компоновка использует фитинг по ширине Stretch , чтобы растянуть каждую кнопку, чтобы она равномерно вписывалась в
контейнер. Центральная кнопка имеет дочерний компонент макета со значением maxWidth , равным 64, поэтому он не будет растягиваться.