Линейная скорость | формула и расшифровка

4343

3

20.05.2022

3 мин. на чтение

Понимание любого понятия в физике предполагает расшифровку определения связанных терминов. Таким образом, в случае линейной скорости становится необходимым определить линейную скорость и скорость по отдельности.

Линейная скорость относится к движению объекта по прямой линии или по заданной оси. С другой стороны, скорость означает расстояние, которое движущееся тело проходит в определенном направлении за определенное время. Таким образом, сочетание этих двух определений поможет вам понять основную концепцию линейной скорости.

Что такое скорость?

Термин «скорость» может использоваться в различных областях, включая физику, термодинамику, химию и т. д. Прежде чем мы перейдем к пониманию линейной и угловой скорости, мы сначала определим скорость как отдельный термин.

Скорость можно объяснить как скорость изменения положения объекта в течение определенного срока или диапазона времени, ее можно разделить на два типа: угловая скорость и линейная скорость. Чтобы определить скорость, мы возьмем пример, поэтому представьте, что вы едете по дороге и смотрите на приборную панель или любые вывески во время движения, спидометр показывает, что автомобиль движется со скоростью 65 км в час, тогда мы можем сказать, что скорость 65 км в час — это скорость, которая представляет собой скорость изменения км по отношению к часам, которые мы видим. Формула скорости равна расстоянию, деленному на время, может рассчитать линейную скорость объекта. В формуле v обозначает линейную скорость, d обозначает пройденное расстояние, а t обозначает время.

Теперь, возвращаясь к ее различным типам, линейная скорость — это просто скорость изменения положения объекта, который движется по прямому пути, поэтому любой движущийся объект имеет линейную скорость, с другой стороны, угловая скорость применяется только или может применяться к объектам, которые движутся по круговой траектории, а также может быть определена как скорость изменения углового смещения во времени.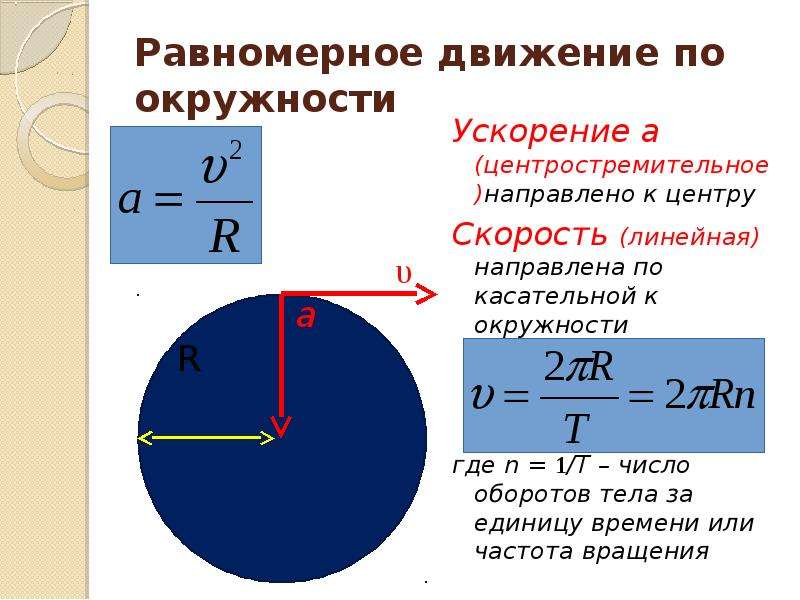 Угловая скорость, измеряемая в рад/с, которая также может быть преобразована в градусы, представляет собой изменение угла во времени. v=rω для расчета линейной скорости по угловой скорости.

V = ωr, где ω равно радианам в секунду, а r — радиус.

Если период вращения равен t, то ω=^2π/_t. Как результат, v=^2π∗r/_t.

Линейную скорость можно испытать в повседневной жизни, поскольку мы видим так много движущихся объектов, которые имеют линейную скорость, таких как человек, идущий на прогулку, вождение, бег или езду на велосипеде, всегда может быть линейная скорость, которая может наблюдаться. Кроме того, бывают случаи, когда объект может двигаться по прямому пути с заданной постоянной скоростью, это можно сказать, что объект движется с постоянной линейной скоростью, проще говоря, мы можем сказать, что скорость Лены объекта не изменяется и, следовательно, постоянный. Линейная скорость, измеряемая в м/с, — это скорость по прямой.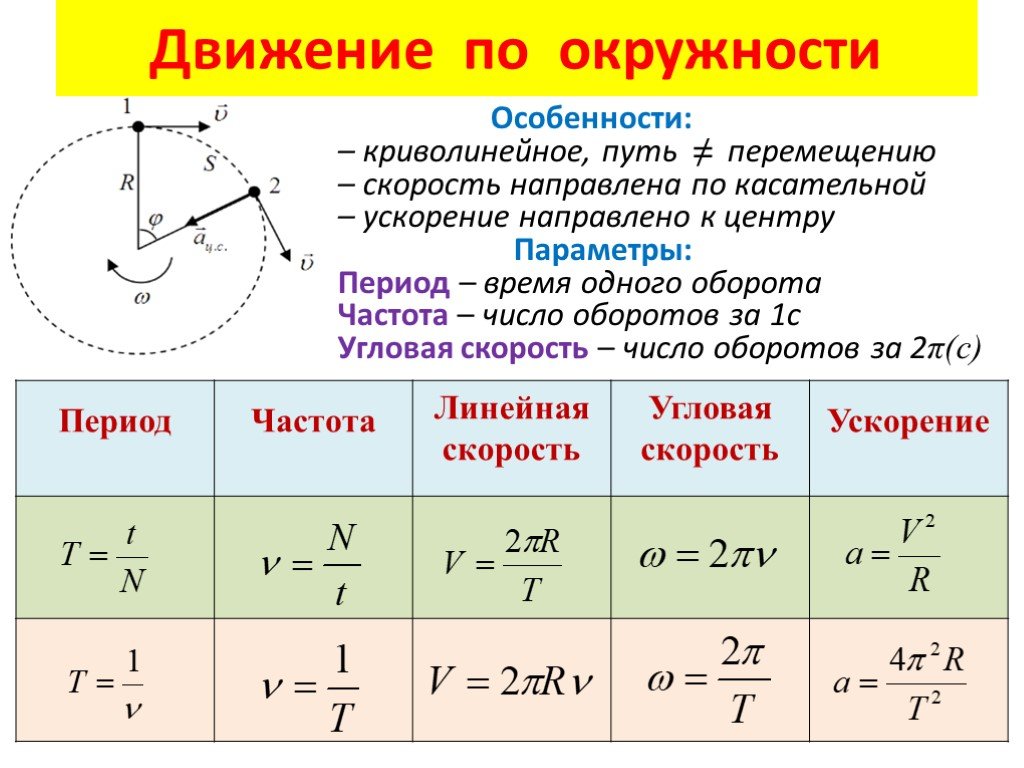

Когда мы говорим об окружности, связь между дугой на окружности и углом, на который она опирается, измеренным в излучении, позволяет нам определить величины, связанные с движением по окружности, и благодаря этому также мы можем сказать, что объекты, движущиеся по круговой траектории, относятся к типу 2. скорости, когда линейна, а другая — угловая скорость, как упоминалось выше. В дополнение к этому мы также можем понимать равномерное круговое движение. Равномерное круговое движение может определять линейную скорость, которая измеряет изменение длины дуги с течением времени.

Когда мы говорим о круговом движении, мы также говорим о направлении линейной скорости. Теперь направление скорости частицы Салина является тангенциальным к круговому пути, который мы видим в любой данной точке этого кругового движения. Направление играет очень важную роль в определении изменения характеристик, скорость является физической векторной величиной, что означает, что для ее правильного определения требуются как величина, так и направление, поэтому, если происходит изменение скорости, направления или того и другого, меняется философия объекта, и тогда мы говорим, что объект является ускоренным движением или ускоряется.

Что такое линейная скорость? 

В самом основном смысле определение линейной скорости связано с измерением скорости объекта, когда он движется в определенном направлении. Следовательно, это относится к смещению объекта во времени. 

Однако объект должен двигаться по определенной прямой линии. Единицей линейной скорости в системе СИ является метр в секунду или м/с (мс- ¹ ). 

С другой стороны, размерная формула линейной скорости имеет вид M ⁰ L ¹ T ¹

Кроме того, вы должны знать, что это векторная величина, что указывает на то, что она имеет направленный характер. 

Какая формула линейной скорости? 

Нет никаких различий между обычной скоростью и линейной скоростью, поскольку обе они являются векторными величинами. 

Следовательно, формула линейной скорости –  ν = d/t

Например, предположим, что движущийся объект преодолевает расстояние 500 метров по прямой линии за 10 секунд. В этом случае линейная скорость объекта равна – 

ν = 500 метров/10 секунд = 50 м/с или 50 мс- ¹ . 

Логически говоря, линейная скорость также применяется к объекту, который движется в круговом направлении, следуя геометрическому месту. В этом случае она называется угловой скоростью. 

Криволинейное движение

Как рассчитывается линейная скорость?

Оглавление

Время чтения: 
4 минуты

632

Интуитивное понятие о скорости мы получаем ещё с детства. Например, глядя в окно или находясь на улице отмечаем про себя, что некоторые из людей идут быстрее, чем другие, а машины на проезжей части движутся быстрее, чем любой из пешеходов. Однако для физики, как науки, такого, бытового понимания о скорости недостаточно, поэтому вводится её точное определение.

Понятие скорости

Скоростью материальной точки (тела) при равномерном движении называется физическая величина, показывающая, какой путь точка (тело), проходит за единицу времени.

Подчеркнём, что речь идёт именно о пути, а не о перемещении. Перемещением называется вектор, соединяющий точку начала и точку конца движения. Его величина равна расстоянию между этими точками. Путь представляет собой длину траектории, по которой происходило движение. Наглядно это можно показать на рисунке.

Рис.1 Красная стрелка – перемещение. Коричневая кривая – путь.

Равномерным движением называют движение, при котором за одинаковые промежутки времени тело проходит одно и то же расстояние. Направление движения при этом может изменяться. В качестве примера можно привести равномерное перемещение точки по окружности.

Формула понятия скорости следующая:

\[\overline{\mathrm{v}}=s / t\]

Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.

Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.

Из приведённой формулы очень легко найти размерность скорости. Т. к. расстояние измеряется в метрах, а время в секундах, то единицей скорости будет метр в секунду м/с. Отметим, что на практике часто скорость измеряют не в метрах в секунду, а, например, в километрах в час.

Существует ещё так называемая средняя скорость – скалярная величина, равная скорости, с которой бы тело перемещалось, если бы преодолевало путь, двигаясь равномерно.

Примеры

Поезд длиной 300 метров, двигаясь равномерно, проезжает тоннель длиной 420 метров за 3 минуты. Найти скорость поезда.

Решение:
Длину поезда обозначим через l, а длину тоннеля через L.
Словосочетание «проезжает тоннель за 3 минуты» означает, что это время поезд входит в тоннель кабиной машиниста и выходит с концом последнего вагона. Пройденное им расстояние S в таком случае является суммой длины тоннеля и длины поезда.
\[S = I + L = 300 + 420 = 720 м/с.\]
Скорость поезда – это скорость любой из его точек. Для простоты будем считать, что это скорость кабины машиниста.
Переводим минуты в секунды: 3 * 60 = 180с.
Скорость получаем, разделив перемещение на время: 720/180 = 4 м/с.

Ответ: Скорость поезда равна 4 м/с.

Машина 3 часа едет со скоростью 4 км/ч, затем 4 часа со скоростью 61,2 км/ч. Требуется найти среднюю скорость движения машины на всем её пути.

Решение:
Обозначим время движения машины со скоростью 4 км/ч, как \[t_{1}\], а время движения машины со скоростью 61,2 км/ч, как \[t_{2}\].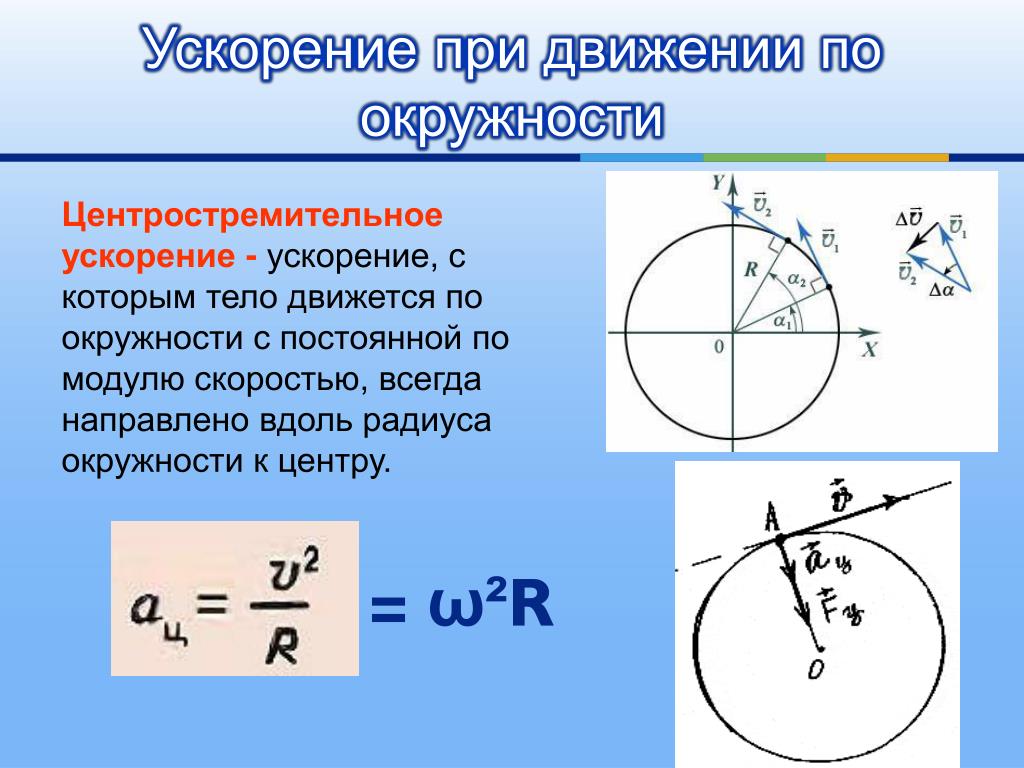
Находим общий путь, который проехала машина. Обозначим его, как S. Общий равен сумме путей, которые ехала машина со скоростью 58,4 км/ч и 61,2 км/ч. Первый из них обозначим как \[S_{1}\], он равен \[S_{1}\] = 3*58,4 = 175,2 км
Второй из них обозначим как S2, он равен: \[S_{2} = 4*61,2 = 244,8 км\]
Складываем эти расстояния и получаем: S = 175,2 + 244,8 = 420 км
Это есть весь путь, пройденный нашей машиной.
Общее время t, которое она потратила будет \[t = t_{1} + t_{2} =3 + 4 = 7 ч\]
Чтобы узнать среднюю скорость, делим общее расстояние на общее время v = S/t = 420/7 = 60 км/ч.

Ответ: Средняя скорость машины равна 60 км/ч.
Обращать время в секунды, а скорость в метры в секунду здесь смысла не имеет, можно и так получить нужное решение.

Линейная скорость

Линейной скоростью именуют величину равную пути, проходимым телом за единицу времени. Движение тела при этом может быть как прямолинейным так и совершаться по криволинейной траектории, например, окружности. Отметим, что линейная скорость всегда направлена по касательной к траектории.

Формул для расчета линейной скорости существует множество, но общей можно назвать:

\[v=S / t\]

S – путь, который прошло тело, t – время, которое оно на это потратило.

Если тело вращается по окружности, то путь, проходимый им, равен её длине. Как известно из геометрии, указанная величина равна 2πR, где R – радиус окружности. Отсюда легко сообразить, что линейная скорость тела при равномерном движении по окружности будет \[\boldsymbol{v=2 \pi R / T}\].

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

О связи между линейной и угловой скоростями

Угловой скоростью называется векторная величина, показывающая, насколько быстро и в каком направлении вращается материальная точка или тело относительно центра вращения.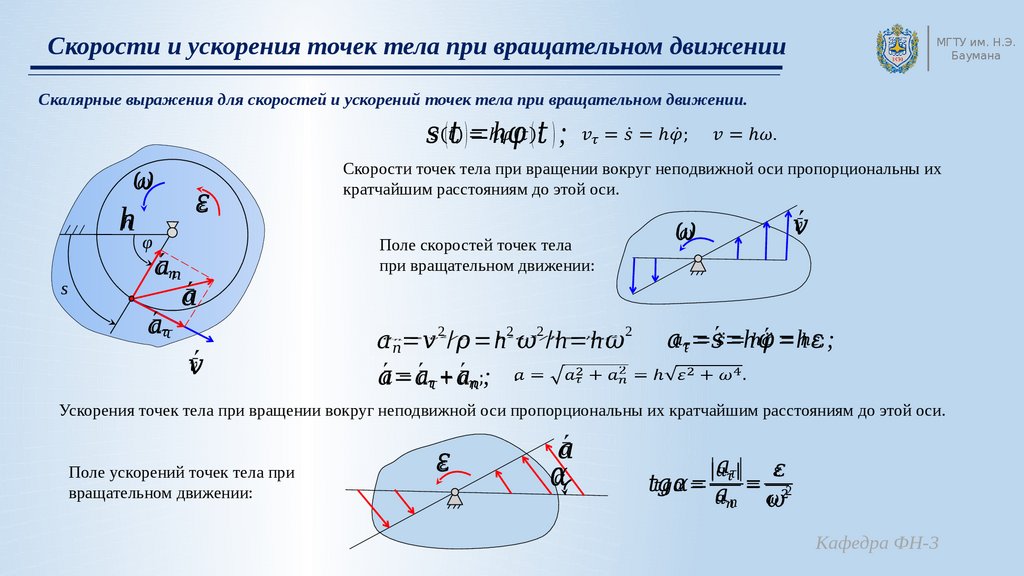 {2} R\]

Оценить статью (39 оценок):

Поделиться

Формула тангенциального ускорения — определение, формула линейного ускорения и примеры решения

Понятие тангенциального ускорения используется для измерения изменения тангенциальной скорости точки определенного радиуса с изменением времени. Линейное и тангенциальное ускорения одинаковы, но в тангенциальном направлении, что приводит к круговому движению. Тангенциальное ускорение определяется как скорость изменения тангенциальной скорости вещества на круговом пути. 9{2}}\конец{массив} \)

Или

\(\begin{array}{l}a_{t}=v.\frac{dv}{ds}\end{array} \)

Обозначения, используемые в формуле

• a _t тангенциальное ускорение
• Δv — изменение угловой скорости
• Δt изменение во времени
• v — линейная скорость
• с — пройденное расстояние
• t это время

Формула тангенциального ускорения используется для расчета тангенциального ускорения и связанных с ним параметров в единицах измерения м/с ²

Формула линейного ускорения

Линейное ускорение определяется как равномерное ускорение, вызванное движением тела по прямой линии. Есть три уравнения, которые важны для линейного ускорения в зависимости от таких параметров, как начальная и конечная скорость, смещение, время и ускорение.

Ниже приведена таблица, объясняющая все три уравнения, которые используются в линейном ускорении:

Обозначения, используемые в формуле

• u начальная скорость
• а это ускорение
• t это время
• v — конечная скорость
• с это ускорение

Решенный пример

Пример 1:

При скорости от 20 м/с до 80 м/с за 30 с тело равномерно ускоряется на круговой траектории. Рассчитайте ускорение по касательной.

Решение:

Заданные параметры

v _i = 20 м/с

v _f = 80 м/с
d _v = v _f – v _i = 80 – 20 = 60 м/с

d _t = t _f – t _i = 30 – 0 = 30 сек

Формула тангенциального ускорения

a _t = d _v / d _t

а _т = 60/30

а _t = 2 м/с ²

Оставайтесь с нами, чтобы узнать больше о концепциях, связанных с физикой.

5.3 Угловое ускорение – биомеханика движений человека

Угловое ускорение обозначается греческой буквой альфа (α). Угловое ускорение представляет собой скорость изменения угловой скорости во времени. Другой способ подумать об этом — как быстро что-то ускоряется или замедляется.

ускорение (α) = Δω/Δt

Единицы измерения: рад/с ² или градусов/с ² . Когда скорость увеличивается, ускорение происходит в том же направлении вращения, чтобы увеличить скорость. Когда скорость уменьшается, должно быть ускорение в направлении, противоположном движению, действующее как тормоз, чтобы уменьшить скорость.

Ускорение имеет направление. Если объект движется в направлении против часовой стрелки (+) и набирает скорость, ускорение положительное. Если скорость уменьшается, ускорение отрицательно. Если объект движется по часовой стрелке (-) и набирает скорость, ускорение отрицательно. Если скорость уменьшается, ускорение положительно.

Пример 1. Расчет углового ускорения и замедления велосипедного колеса

Предположим, подросток кладет велосипед на спину и запускает вращение заднего колеса из состояния покоя до конечной угловой скорости 250 об/мин за 5,00 с. (a) Рассчитайте угловое ускорение в рад/с ² . (b) Если теперь она ударит по тормозам, вызывая угловое ускорение 90 105 -87,3 рад/с 90 053 2 90 054 90 106 , сколько времени понадобится колесу, чтобы остановиться?

Стратегия для (a)

Угловое ускорение можно найти непосредственно из его определения в [latex]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}[/latex] потому что конечная угловая скорость и время заданы. Мы видим, что Δω — это 250 об/мин, а Δ t — это 5,00 с.

Решение задачи (a)

Введя известную информацию в определение углового ускорения, получим

[латекс]\begin{array}{lcl} \boldsymbol{\alpha} & \boldsymbol{=} & \ boldsymbol{\frac{\Delta\omega}{\Delta{t}}} \\ {} & \boldsymbol{=} & \boldsymbol{\frac{250\textbf{об/мин}}{5,00\textbf{с. } }} \end{массив}[/latex]

Поскольку Δω выражается в оборотах в минуту (об/мин), а нам нужны стандартные единицы рад/с ² для углового ускорения, нам нужно преобразовать Δω из об/мин в рад/с:

[ латекс]\begin{массив}{lcl} \boldsymbol{\Delta\omega} & \boldsymbol{=} & \boldsymbol{250\frac{\textbf{rev}}{\textbf{min}}\cdotp\frac{ 2\pi\textbf{ рад}}{\textbf{об}}\cdotp\frac{1\textbf{ мин}}{60\textbf{ сек}}} \\ {} & \boldsymbol{=} & \boldsymbol {26,2\textbf{ рад.}} \end{массив}[/latex] 92} \end{array}[/latex]

Стратегия для (b)

В этой части мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение углового ускорения и решив Δ t , получив

[латекс]\boldsymbol{\Delta{t}\:=}\boldsymbol{\frac{\Delta\ omega}{\alpha}}.[/latex]

Решение для (b)

Здесь угловая скорость уменьшается с 26,2 рад/с 92}} \\ {} & \boldsymbol{=} & \boldsymbol{0.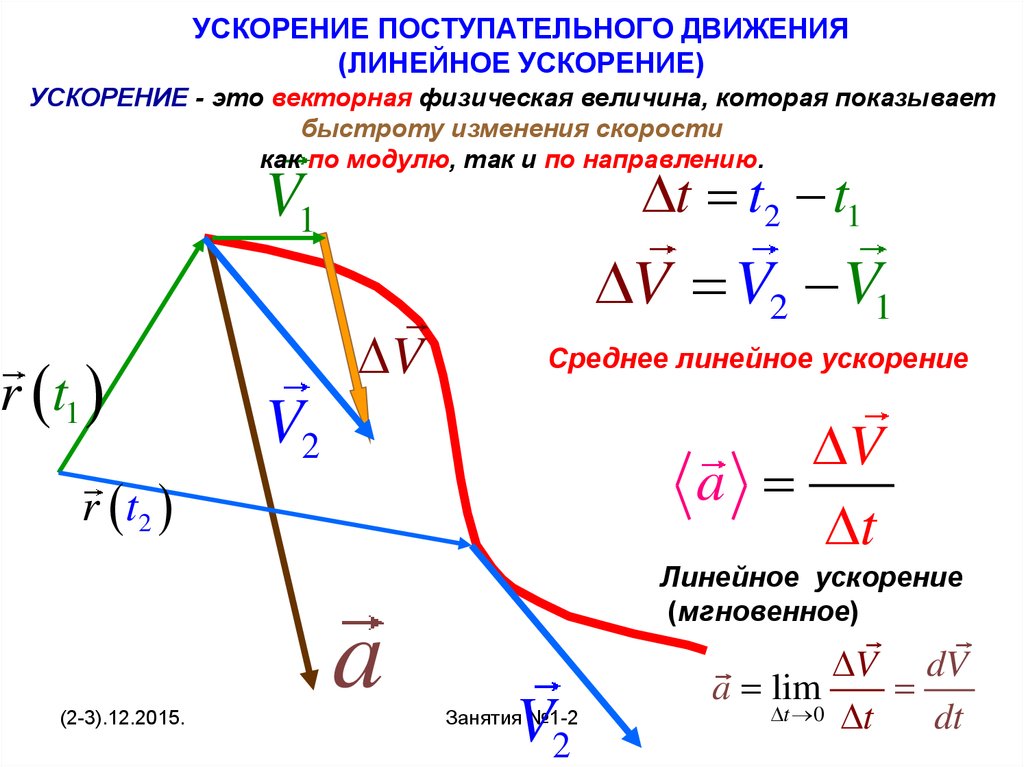 300\textbf{ с.}} \end{array}[/latex]

Обсуждение

Обратите внимание, что угловое ускорение при вращении девушки колесо маленькое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.

Если бы велосипед в предыдущем примере находился на своих колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При движении по окружности линейное ускорение составляет по касательной к окружности в интересующей точке, как показано на рисунке 2. Таким образом, линейное ускорение называется тангенциальным ускорением _т .

Рис. 2. При круговом движении линейное ускорение a возникает при изменении величины скорости: a касается движения. В контексте кругового движения линейное ускорение также называют тангенциальным ускорением a _t .

Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Мы знаем , что при круговом движении центростремительное ускорение a _c относится к изменениям направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рисунке 3. Таким образом, a _t и a _c перпендикулярны и независимы друг от друга. Тангенциальное ускорение a _t напрямую связано с угловым ускорением [латекс]\жирныйсимвол{\альфа}[/латекс] и связано с увеличением или уменьшением скорости, но не с ее направлением.

Рис. 3. Центростремительное ускорение a _c возникает при изменении направления скорости; оно перпендикулярно круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.

Теперь мы можем найти точное соотношение между линейным ускорением a _t и угловым ускорением [латекс]\boldsymbol{\alpha}[/латекс]. Поскольку линейное ускорение пропорционально изменению величины скорости, оно определено как 

[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta{v}}{\Delta{t}}.}[/latex]

Для кругового движения обратите внимание, что v = r ω , так что

[латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}. }[/latex]

Радиус r является постоянным для кругового движения, поэтому Δ( r ω)= r (Δω) . Таким образом,

[латекс]\boldsymbol{a_{\textbf{t}}=r}\boldsymbol{\frac{\Delta\omega}{\Delta{t}}.}[/latex]

По определению [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t}}}.[/latex] Таким образом,

[латекс]\boldsymbol{a_{\textbf{t}}=r\alpha},[/латекс]

или

[латекс] \boldsymbol{\alpha\:=}\boldsymbol{\frac{a_{\textbf{t}}}{r}.}[/latex]

Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес велосипеда, тем больше ускорение велосипеда. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении [латекс]\boldsymbol{\alpha}[/латекс].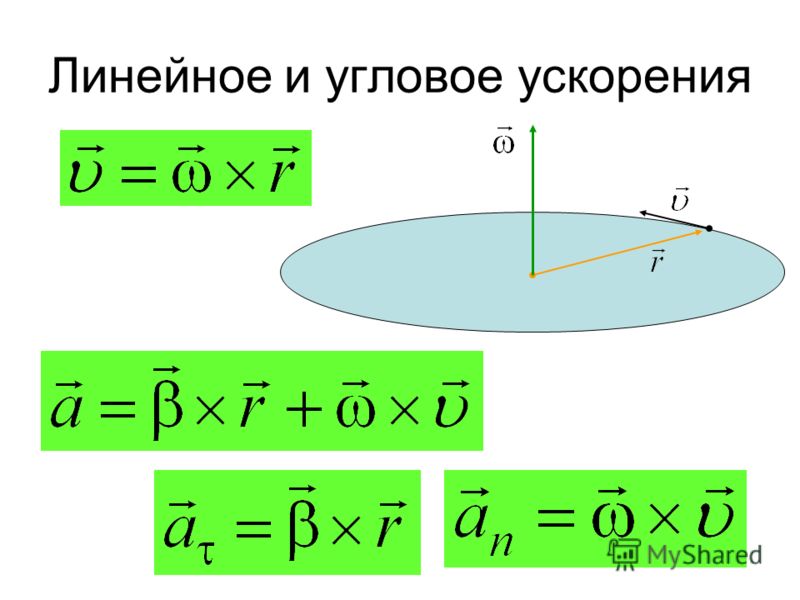

До сих пор мы определили три величины вращения — θ , ω и [латекс]\жирныйсимвол{\альфа}[/латекс]. Эти величины аналогичны поступательным величинам x , v и a . В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.

Ротационный	Перевод	Отношения
[латекс]\boldsymbol{\theta}[/латекс]	[латекс]\boldsymbol{x}[/латекс]	[латекс] \boldsymbol{\theta=\frac{x}{r}}[/латекс]
[латекс]\boldsymbol{\omega}[/латекс]	[латекс]\boldsymbol{v}[/латекс]	[латекс]\boldsymbol{\omega=\frac{v}{r}}[/латекс]
[латекс]\boldsymbol{\alpha}[/латекс]	[латекс]\boldsymbol{a}[/латекс]	[латекс] \boldsymbol{\alpha=\frac{a_{\textbf{t}}}{r}}[/latex]
Таблица 1. Вращательные и поступательные величины.

• Равномерное круговое движение — это движение с постоянной угловой скоростью [латекс]\жирныйсимвол{\омега=\фракция{\Delta\theta}{\Delta{t}}}.[/latex]
• При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т.е. углового ускорения) равна [латекс]\boldsymbol{\alpha=\frac{\Delta\omega}{\Delta{t} }}.[/латекс]
• Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, задается как [латекс]\жирныйсимвол{а_{\textbf{t}}=\frac{\Delta{v}}{\Delta{t} }}.[/латекс]
• Для кругового движения обратите внимание, что v = r ω , так что

  [латекс]\boldsymbol{a_{\textbf{t}}\:=}\boldsymbol{\frac{\Delta(r\omega)}{\Delta{t}}}.[/latex]

• Радиус r постоянен для кругового движения, поэтому Δ( r ω)= р Δω .