БэбиБлог — беременность, календарь беременности, дневники
Отказ от прикорма
Здоровье новорожденных
Здравствуйте. Девочки помогите. Малой 9 месяцев. Пухляш и аппетит был отменный. Прикорм кушала все что дам и грудью запивала. Зубов 8 штук и прорезывались без проблем. Вдруг резко отказывается от прикорма! Зубы сцепливает, что ложку в рот не просунуть. И любые продукты-отказ. Только грудь берёт. Были у педиатра, говорит ничего не видит. Горло и
Читать далее
5
Глаза грудничка
Развитие от рождения до года
Здравствуйте, подскажите пожалуйста, может у кого-то было. Ребёнку 2 месяца и бывает что косят глазки. Пройдёт ли это со временем?
13
Интересные сервисы, конкурсы и тест-драйвы от крупнейших брендов
Розыгрыш цифровой видеоняни Evo Beauty
Результаты будут объявлены 26 июня
«Я выгорала ужасно!»
Смотрите интервью с Викой Дмитриевой
Уход за сухой и очень сухой кожей
Получите бесплатно на тест-драйв
Ты беременна?
Выиграй премиальные роды от Kabrita® в MD GROUP или в Лапино!
Мечты сбываются!!!
Выиграй полное обустройство ванной комнаты от Cersanit
Как совместить работу, учёбу и семью?
Мы собрали для вас полезные статьи об онлайн-обучении в одном разделе
Как понять что у вашего ребенка запор?
Пройдите наш тест, чтобы развеять сомнения
Ультратонкие вкладыши для груди
Читайте отзывы мам
Врачебная поддержка на Бэбиблоге
Получите мнение врача (бесплатно, только у нас)
Полезное сообщество для мам
Советы, акции, промокоды ждут вас внутри. Присоединяйтесь!
Присоединяйтесь!
Балансир для детей
Воспитание, психология — от года до трех
Здравствуйте,
Сейчас очень часто попадается, что родители покупают вот такой балансир:
Читать далее
7
Никогда не получается 😜😜😜
Кулинарное сообщество
Если уж села за стол, то объелась так что двигаться лень😋
7
Малоежка/нехочуха
Воспитание, психология — от года до трех
Ребенку 1.3 года, со старшим в еде вообще проблем не было, в этом возрасте уплетал еду ложкой или руками. А младший нехочуха, супы мои не ест, второе тоже не ест, каши тоже не особо, чтобы накормить нормальной едой приходится обманом, песнями и пляской, телевизором и телефоном. Зато хорошо ест мясное пюре, видно что моим молоком не наедается, по
Читать далее
6
Когда у вас окрепла шея?
Развитие от рождения до года
Девочки, здравствуйте!
Эта шея мне покоя не дает… Завтра нам 3 месяца. Ходим на массаж и там массажистка сказала что при КС когда доставали ребенка повредили шею, что все кто рожает в Видном, всем калечат детишек. Что очень много дцп из-за этих профессионалов и тд. Короче я на панике теперь..
Ходим на массаж и там массажистка сказала что при КС когда доставали ребенка повредили шею, что все кто рожает в Видном, всем калечат детишек. Что очень много дцп из-за этих профессионалов и тд. Короче я на панике теперь..
Сын хорошо держит голову при бо
Читать далее
31
Пост позлиться или непрошенные советы версия 19999…
Благополучная беременность
Пост позлиться (или поныть?): сижу по работе в мфц, процесс долгий, взяла с собой вязание, вяжу потихонечку дочке шапочку, никого не трогаю: проходит охранница: «ой какая молодец, ни минуты покоя…а кого ждёшь? Девочку наверное?.. и все в таком духе». Отстала в итоге тк я не настроена обсуждать свою беременность с чужими людьми. Проходит 3 минуты
Читать далее
44
Прививки дополнительные
Здоровье новорожденных
Ставим прививки по календарю, но оказывается в календарь не все прививки внесены, например нет от ротовируса, которую ставят до 2 месяцев.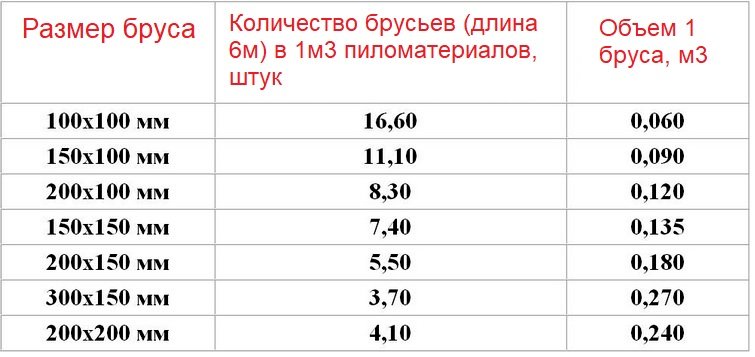 Я не знала о ней и мы
Я не знала о ней и мы
Читать далее
12
Собираю инфу
Семейное здоровье (взрослые)
Я опять про свой живот и кишки.
Для постановки диагноза мне нужно пройти 3 процедуры:
1. ФГДС ( глотание кишки через рот в желудок) . Жуткая процедура. Делала в жизни пару раз, это ужасно(
2. УЗИ брюшной полости. Пару лет назад делала, все было норм.
3. ФКС. А вот это прямо атас. Что-то всовывают в анальное отверстие,&nbs
Читать далее
38
Девочки , у кого на первом скрининге не угадали пол ?
Благополучная беременность
Сегодня было узи . Врач сказала что то торчит , может яички а может клитор . У кого на первом узи сказали пол а потом оказалось по другому ?
27
Эх материнство)))
Здоровье будущей мамы и малыша
Хочу просто сходить в ванную хотя бы на час …
Как много сказано этими словами😂
13
Стала чувствовать приход месячных.
Семейное здоровье (взрослые)
До 1й беременности, после родов, после 2й беременности (зб) и до 3й беременности вообще знать не знала, как там кто-то чувствует приход месячных, ну бывал жор за пару дней до начала и все. Во время месячных тоже дискомфорта никого не было, ну кроме того, что первые 3 дня льёт, как из ведра 😂. После 2х родов месячные начались в 1,2 г
Читать далее
4
Справка 079/У
Дети от шести и старше
Добрый день! Еду с ребенком в дом отдыха, там на ребенка требуется эта справка, причем должно быть указаны анализы на я/гл и осмотр кожн.покровов. В самой форме таких строчек даже нет. Я получила справку в саду, естественно там ни о чем таком ни слова. Придется переделывать, видимо. Анализы мы сдавали в конце мая для справки в бассейн, не хочетс
Читать далее
20
Цвет глаз
Здоровье будущей мамы и малыша
Когда ваши малыши поменяли цвет глаз? И какие у вас с отцом ребенка цвета глаз? На сколько я знаю , все дети рождаются с голубыми глазами и только потов возможно меняют цвет .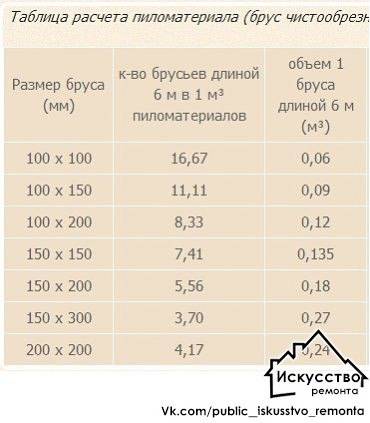 Читаю статьи . Статистика разная
Читаю статьи . Статистика разная
13
Полный ребенок 3 года
Все о детях от трех до шести лет.
Девочки всем привет, беспокоит фигура ребенка🤣. Сейчас ей 3 года, и она весит 18 килограмм. Рост 95. Родилась она 3100. Была на грудном вскармливан
Читать далее
37
Ребенок дерется
Все о детях от трех до шести лет.
Всем привет! Собственно, суть проблемы в заголовке. Дочке 3 года. Драться начала в саду (у них был мальчик, который всех бил и моя научилась). Драки были нечастые, иногда воспитатели жаловались. Сейчас получилось так, что пошли в частный садик (новый), спустя 3 дня директор предложила нам пойти на выход (и это сад за 50 т.р). Дочь дерется, драть
Читать далее
42
При родах врачи не должны давить на живот?
Здоровье будущей мамы и малыша
Читаю некоторые истории здесь и девочки рассказывают , что из них выдавливали ребенка. Но , вроде, так нельзя делать. Тогда зачем делают? Оправдано ли это? Или это старая школа и некомпетентные врачи?
Но , вроде, так нельзя делать. Тогда зачем делают? Оправдано ли это? Или это старая школа и некомпетентные врачи?
25
Малышковый транспорт
Все о детях от трех до шести лет.
Мне очень бы хотелось, чтобы ребенок использовал все виды транспорта: самокат, беговел, велосипед.
Но 1.5 мес разад ребенок наткнулся на ямку и упал с самоката (повредил губу и получил кровоизлияние в зуб, теперь зуб один темнее других).
Самокат отложили. Потому что страшно, что голову расшибет. У нас есть шлем. Но зубы он, наверное,
Читать далее
6
Рюкзак для 3-4 класса
Здравствуй, школа!
Неожиданно не знаем, в какую сторону смотреть) Дочь закончила второй класс и начала тихонько просить новый рюкзак. Сама не знает, что хочет, надо ей помочь) Два года она ходила с рюкзаком Winner One, купленным совсем за недорого и из-за картинки. Я была готова, что даже на один год его хватит. Он, кстати, оказался, прекрасным) Лёгкий, всё
Он, кстати, оказался, прекрасным) Лёгкий, всё
Читать далее
19
Ребёнок засыпает только в плюшевом костюме
Развитие от рождения до года
Малышке почти 7 недель
недавно приезжала Бабуля, у неё Софик отлично засыпала на балконе в плюшевом костюме. Его прелесть в том, что он хорошо фиксирует руки
Читать далее
17
Сколько будет в кубометре — * Выживание в мало-благоприятных Ситуациях * — LiveJournal
?
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор объема
Ниже приведен список калькуляторов объема для нескольких распространенных форм. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».
Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор объема куба
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
|
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.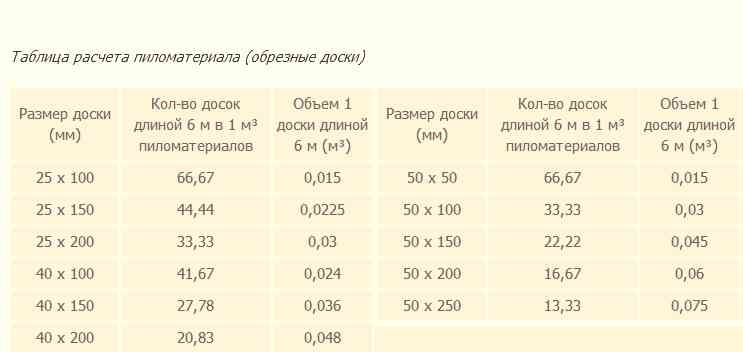
|
Калькулятор объема усеченного конуса
|
Калькулятор объема эллипсоида
|
Калькулятор объема квадратной пирамиды
Калькулятор объема пробирки
|
Связанные Калькулятор площади поверхности | Калькулятор площади
Объем – это количественная оценка трехмерного пространства, занимаемого веществом. Единицей объема в системе СИ является кубический метр, или 9.0253 м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы. Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Единицей объема в системе СИ является кубический метр, или 9.0253 м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы. Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, равноудаленных от заданной точки в его центре, где расстояние между центром и любой точкой на сфере равно радиусу r . Вероятно, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и вычисление их объемов одинаково. Как и в случае с окружностью, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром, д . Уравнение для расчета объема сферы приведено ниже:
| объем = | πr 3 |
EX: Клэр хочет наполнить идеально сферический водяной шар радиусом 0,15 фута уксусом, чтобы использовать его в битве с водяным шаром против ее заклятого врага Хильды в ближайшие выходные. Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:
Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус представляет собой трехмерную форму, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание). На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:
| объем = | πr 2 ч |
где r — радиус, а h — высота конуса
ПРИМЕР: Беа полна решимости выйти из магазина мороженого с хорошо потраченными 5 долларами, заработанными тяжелым трудом. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее. Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:
Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее. Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйма 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет < 15%, и решает купить сахарный рожок. . Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых сходятся в каждой из его вершин и все перпендикулярны соответствующим соседним граням. Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр. Ниже приведено уравнение для расчета объема куба:
Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр. Ниже приведено уравнение для расчета объема куба:
объем = а 3
где a — длина ребра куба
ПРИМЕР: Боб, родившийся в Вайоминге (и никогда не покидавший штат), недавно посетил родину своих предков в Небраске. Потрясенный великолепием Небраски и окружающей средой, непохожей ни на что другое, с чем он когда-либо сталкивался ранее, Боб понял, что ему нужно привезти часть Небраски домой с собой. У Боба есть кубический чемодан с длиной ребра 2 фута, и он вычисляет объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной прямой оси. Однако в обычном употреблении «цилиндр» относится к прямолинейному круговому цилиндру, основаниями которого являются окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой 90 253 h 90 256 и радиусом 90 253 r 90 256. . Уравнение для расчета объема цилиндра показано ниже:
. Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
ПРИМЕР: Кэлум хочет построить замок из песка в гостиной своего дома. Поскольку он решительно выступает за переработку отходов, он нашел три цилиндрические бочки с незаконной свалки и очистил их от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя приведенное ниже уравнение:
объем = π × 3 2 × 4 = 113,097 футов 3
Он успешно строит замок из песка в своем доме и, в качестве дополнительного бонуса, ему удается экономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте. темнота.
Прямоугольный резервуар
Прямоугольный резервуар представляет собой обобщенную форму куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем= длина × ширина × высота
ПРИМЕР: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к тортам. Она планирует пройти по тропе Калалау на Кауаи, и, хотя Дарби в отличной форме, она беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет наполнить свой идеально прямоугольный пакет длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитывается ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы. Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + ч) |
где r радиус и h высота цилиндрической части
Джо может взять с собой капсулу времени, которую он хочет похоронить для будущих поколений в своем путешествии самопознания через Гималаи:
объем = π × 1,5 2 × 3 + 4/3 × π ×1,5 3 = 35,343 футов 3
Сферическая крышка
Сферическая крышка представляет собой часть сферы, отделенную от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая шапка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера разделена на две параллельные плоскости и два разных радиуса, где плоскости проходят через сферу. Уравнение для расчета объема сферической шапки получено из уравнения для сферического сегмента, где второй радиус равен 0. Относительно сферической шапки, показанной в калькуляторе:
Уравнение для расчета объема сферической шапки получено из уравнения для сферического сегмента, где второй радиус равен 0. Относительно сферической шапки, показанной в калькуляторе:
| объем = | πh 2 (3R — h) |
Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Дано r и R : h = R ± √R 2 — r 2
| Дано r и 9025 3 часа : R = |
|
| объем = | πh(r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
таким образом, чтобы мороженое оставалось упакованным внутри конуса, а поверхность мороженого находилась на одном уровне и была параллельна плоскости отверстия конуса. Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:
Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10,849 дюйма 3
Эллипсоид
Эллипсоид является трехмерным аналогом эллипса, и поверхность, которую можно описать как деформацию сферы за счет масштабирования направленных элементов. Центром эллипсоида называется точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным. Уравнение для расчета объема эллипсоида выглядит следующим образом:
| объем = | πabc |
где a , b и c длины осей мясо, поскольку он может поместиться в булочке в форме эллипса. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:
Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:
объем = 4/3 × π × 1,5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии представляет собой трехмерное тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это фигура на плоскости, ограниченная конечным числом отрезков прямой линии. Существует множество возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание — квадрат. Другое различие, связанное с пирамидами, связано с расположением вершины. Вершина правильной пирамиды находится прямо над центром тяжести ее основания. Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды можно записать как:
Обобщенный объем пирамиды:
| объем = | ч/б |
где b площадь основания и h высота
Объем квадратной пирамиды:
| объем = | а 2 ч |
где a длина края основания
ПРИМЕР: Ван очарован древним Египтом и особенно любит все, что связано с пирамидами. Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:
Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:
объем = 1/3 × 5 2 × 12 = 100 футов 3
Трубчатая пирамида
Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газов. . Вычисление объема трубы по существу использует ту же формулу, что и для цилиндра ( объем = pr 2 h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина используется, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
| объем = π |
| л |
где d 1 — внешний диаметр, d 2 — внутренний диаметр, l — длина трубы
EX: Beulah посвящен охране окружающей среды. Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу, через ручей. Он хочет более легкого доступа к своему дому и просит Беулу построить ему дорогу, обеспечив при этом свободное течение ручья, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые плотины были бы хорошей точкой для прокладки трубы через ручей. Объем запатентованного ударопрочного бетона, необходимый для строительства трубы с внешним диаметром 3 фута, внутренним диаметром 2,5 фута и длиной 10 футов, можно рассчитать следующим образом:
Объем запатентованного ударопрочного бетона, необходимый для строительства трубы с внешним диаметром 3 фута, внутренним диаметром 2,5 фута и длиной 10 футов, можно рассчитать следующим образом:
| объем = π × |
| × l0 = 21,6 фута 3 |
Общие единицы объема
Диагональ формулы куба
Диагональ формулы куба помогает в вычислении длин различных диагоналей куба — диагоналей грани и диагоналей тела. Куб — это трехмерная объемная фигура, также известная как квадратное тело, все грани которой имеют одинаковую меру. Это означает, что длина, ширина и высота куба равновелики, а каждая его грань — квадрат. Давайте узнаем больше о диагонали куба и диагонали куба формулы для измерения длин диагоналей лица и диагоналей тела с примерами.
Что такое диагональ куба?
Диагональ куба — это отрезок, соединяющий любые две несмежные вершины куба. Куб — одна из важных геометрических фигур, потому что эта трехмерная форма имеет все 12 равных граней, и это одна из наиболее часто встречающихся фигур вокруг нас. Некоторыми из реальных примеров куба являются кубики льда, кубики сахара, кубики Рубика, игральные кости и т. д. В кубе есть два вида диагоналей, потому что это трехмерная фигура.
Диагональ грани куба
Куб имеет 6 граней квадратной формы. На каждой грани есть две диагонали, соединяющие несмежные вершины. Следовательно, у куба 12 диагоналей граней.
Диагональ тела куба
Диагонали тела соединяют противоположные вершины куба, проходящие через тело куба. Следовательно, в кубе есть 4 диагонали тела, которые проходят через куб, соединяющий противоположные углы.
Формула диагонали куба
Длину диагоналей куба можно рассчитать по заданным параметрам и требованиям.
Длина диагонали грани куба
Формула, используемая для расчета длины диагонали грани куба, выражается следующим образом:
Длина каждой диагонали грани куба = √2a , где a = Длина каждой стороны куба.
Пример: Найдите длину диагонали грани куба, если длина его стороны равна 6 см.
Решение:
Дано, длина стороны куба (а) = 6 см, Диагональ грани = ?
Длина каждой диагонали грани куба = √2a
Итак, подставим данное значение в формулу.
Длина каждой диагонали грани куба = √2a
⇒ √2a ⇒√2 × 6 = 8,48 см
Следовательно, длина диагонали грани равна 8,48 см
Длина диагонали тела куба
формула, которая используется для расчета длины диагонали пространства или тела куба, задается как
Длина каждой диагонали тела куба = √3a , где a = длина каждой стороны куба.
Пример: Найдите длину диагонали тела куба, если длина его стороны равна 7 дюймов.
Решение:
Дана длина стороны куба (а) = 7 дюймов, диагональ тела = ?
Длина каждой диагонали тела куба = √3a
Итак, подставим данное значение в формулу.
Длина каждой диагонали тела куба = √3a
⇒ √3a ⇒√3 × 7 = 12,12 дюйма.
Следовательно, длина диагонали тела равна 12,12 дюйма.
Вывод формулы диагонали куба
Диагональ формулы куба обычно относится к диагонали тела куба. Эту формулу можно вывести, используя теорему Пифагора.
Обозначим сторону куба как ‘a’, диагональ грани как r и диагональ тела как d. Как только мы соединим диагональ лица и диагональ тела, мы увидим, что образуется прямоугольный треугольник со сторонами a, r и d. Диагональ тела становится гипотенузой образующегося прямоугольного треугольника.
Используя теорему Пифагора, мы имеем 2 + r 2 = d 2 (давайте сохраним это как уравнение 1)
Мы уже знаем, что диагональ грани равна √2a, поэтому, ‘ r’ можно заменить на √2a, это означает, что ‘r’ = √2a
Подставляя значение r в уравнение 1, мы получаем
a 2 + (√2a) 2 = d 2
a 2 + 2a 2 = d 2
3a 2 = d 2
d = √(3a 2 )
d = √3a
Следовательно, формула диагонали куба = √3a
9000 2 Разбейте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Записаться на бесплатный пробный урок
Примеры с использованием формулы вычисления диагонали куба
Пример 1. Вычислите длину диагонали куба, каждая сторона которого равна 5 единицам.
Решение:
Дана длина каждой стороны куба (а) = 5 единиц; диагональ тела = ?
Итак, подставим данные значения в формулу
Длина диагонали тела куба = √3a
= √3 × 5 = 8,66 ед. = 8,66 ед.
Пример 2: Длина диагонали куба равна 8√3 единиц. Найдите длину каждой стороны куба.
Решение:
Дано, диагональ тела = 8√3 единиц; длина каждой стороны куба (а) = ?
Мы знаем, что формула диагонали тела куба выражается как
Длина диагонали тела куба = √3a
Итак, давайте подставим данные значения в формулу, чтобы получить неизвестное значение,
Длина диагонали тела куба = √3a
⇒ 8√3 = √3a
⇒ a = 8
Следовательно, длина каждой стороны данного куба = 8 единиц
Пример 3. Найдите длину диагонали грани куба, если длина стороны куба равна 6 единицам. Используйте формулу диагонали грани куба.
Найдите длину диагонали грани куба, если длина стороны куба равна 6 единицам. Используйте формулу диагонали грани куба.
Решение:
Дана длина каждой стороны куба (а) = 6 единиц, диагональ грани = ? Используя формулу диагонали грани куба,
Длина каждой диагонали грани куба = √2a
⇒ √2 × 6 = 8,49 единицы
Следовательно, длина диагонали грани куба составляет 8,49 единицы.
Часто задаваемые вопросы о формуле диагонали куба
Что такое диагональ куба?
Диагональ куба — это отрезок, соединяющий любые две его несмежные вершины. Поскольку куб представляет собой трехмерную форму (3D-форму), он имеет два вида диагоналей — диагонали грани и диагонали тела. Диагональ грани — это диагональ, образованная 6 гранями куба. А так как на каждой грани можно образовать две диагонали, значит в кубе 12 диагоналей граней. Если говорить о диагоналях тела, то мы знаем, что оно пересекает центр куба, а значит, в кубе можно составить 4 диагонали тела.
Что такое Диагональ формулы куба?
Диагональ куба Формула помогает в измерении диагоналей куба. Так как куб имеет два вида диагоналей, есть 2 разные формулы для вычисления их значения.
- Диагональ грани куба формула = √2a; где а = длина каждой стороны куба.
- Диагональ тела формулы куба = √3a; где а = длина каждой стороны куба.
По какой формуле найти диагональ грани куба?
Формула для расчета длины диагонали грани куба выражается следующим образом: Длина каждой диагонали грани куба = √2a, где a = длина каждой стороны куба
Какая формула для вычисления диагонали куба куб?
Формула для расчета длины диагонали тела или главной диагонали куба представлена в виде: Длина диагонали тела куба = √3a, где a = длина каждой стороны куба
Используя диагональ Формула куба, Найдите длину диагонали со стороной, равной 8 единицам.
Длину диагонали тела куба можно рассчитать по формуле диагональ тела куба = √3a.

 Поэтому полезно будет узнать эти нормативы и пользоваться ими при покупке. В 1 куб.м должно содержаться:
Поэтому полезно будет узнать эти нормативы и пользоваться ими при покупке. В 1 куб.м должно содержаться: Он отрезает идеальный сферический колпачок от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:0003
Он отрезает идеальный сферический колпачок от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:0003