Виды профиля и размеры профилированного бруса, отличия во влажности и ноу-хау в производстве

Содержание:

• Размер профилированного бруса
• Виды профиля
• Структура материала
• Внешний вид
• Влажность материала

Как любой другой материал, профилированный брус имеет несколько видов, каждый из которых имеет ряд преимуществ и недостатков. Виды профилированного бруса давно обсуждаются на форумах и строителями. Сложно склониться в пользу одного из них, так как ассортимент этой продукции велик и многие виды начали использовать не так давно. Они еще не показали себя, и неизвестно, как будет выглядеть дом из такого товара через 30-40 лет.

Содержание статьи:

• 1 На какие виды делится?
• 2 Размер профилированного бруса
  • 2.1 Толщина 100 мм
  • 2.2 Толщина 150 мм
  • 2.3 Толщина 200 мм
• 3 Виды профиля
• 4 Структура материала
  • 4.1 Теплый брус
• 5 Внешний вид
• 6 Влажность материала

На какие виды делится?

Обо всех достоинствах и недостатках профилированного бруса мы уже говорили. Но не многие знают, что под понятием «профилированный брус» скрывается огромное множество видов этого товара.

Все отличия видов профилированного материала можно разделить по признакам:

1. Размер профилированного звена. Он может иметь различную длину и сечение.
2. Вид профиля. Гребенка, двойной, финский и т.п.
3. Структура материала. Из цельного массива дерева и клееный профилированный брус, теплый.
4. Внешний вид. Может иметь прямолинейную лицевую сторону или D- образную.
5. Сушеный или естественной влажности.

Все виды профилированного бруса должны соответствовать ГОСТу 8242-88. Давайте разберемся подробнее в этих видах.

Размер профилированного бруса

Весь подобный материал бывает нескольких размеров, которые указанны в ГОСТе. Конечно, изготовители идут навстречу покупателю и могут изготовить профилированный пиломатериал индивидуального размера. Но существуют определенные стандарты: 100х100, 100х150, 150х150, 150х200, 200х200. Основной показатель это толщина в 100, 150, 200 мм.

Рассмотрим каждый по толщине отдельно.

Толщина 100 мм

Такой тип сечения пиломатериала применяют для строения легких деревянных конструкций. Например: баня, беседка, веранда. Толщина в 100 мм не дает возможность строить из него жилые дома. Хотя если вы строите дачный домик и собираетесь использовать его только в летнее время, такой толщины достаточно. В кубе пиломатериала такой толщины обычно: 100х150 – 11шт., 100х200 – 8 шт. Профиль у такого вида обычно два шипа — два паза.

Толщина 150 мм

Такое сечения товара подходит для строительства жилого дома, так как он уже толще чему у бруса 100х150, но в тоже время он дешевле сечения 200х200. В кубе такого пиломатериала: 150х150 – 7,4 шт., 150х200 – 5,5 шт. В таком виде профилированного бруса уже используют профиль в виде гребенки. Это не дает промерзнуть домам из такого товара.

Толщина 200 мм

Профессионалы ля строительства больших жилых домов любят использовать именно этот размер профилированного товара. Такой вид имеет высокое сопротивление стен и подходит для строительства коттеджей. Самым распространенным материалом считается профилированный пиломатериал сечением 200х150, 200х200 мм. В кубе такого товара: 200х150 – 5,5 шт., 200х200 – 4 шт. Стоит такой вид дороже, но в зимнее время существует гибкая система скидок.

Длина стандартного профилированного пиломатериала 6 м. Изготовление по гостам придерживаются фирмы, которые отвечают за качество своего товара. Дома из профилированного бруса могут иметь очень сложную конструкцию, и производитель идет навстречу заказчику, изготавливая материал по индивидуальным размерам. Длина тоже изготавливается под индивидуальный вид проекта.

Виды профиля

Профилированный брус имеет основное отличие от простого — это профиль. Профиль вырезается на станках по специальным шаблонам. Большое значение при выборе профилированного пиломатериала имеет вид профиля. Профиль, выставленный на рынке, имеет большой ассортимент, но и тут есть свои стандарты. По своему виду профиль бывает:

1. Профиль с одним шипом.
2. Профиль с двумя шипами.
3. Профиль со скошенными фасками.
4. Профиль с большим количеством шипов – «гребенка».
5. Финский профиль.

Для жилого дома рекомендуется использовать этот пиломатериал — «гребенка». Такой профиль создает надежный барьер для проникновения холода и влаги. Если строение имеет легкую конструкцию, то подойдет профиль в один-два шипа.

Особо хочется отметить финский профиль. Он появился на рынке России совсем недавно. Пришел он к нам не из Финляндии. Просто качество такого пиломатериала велико, как и дома фонов. На нижней части заготовки делают один большой широкий паз, а сверху шип образованный двумя параллельными полосами. Паз при этом имеет глубину большую, чем у обычного профиля. При соединении сырья с финским профилем происходит более плотное примыкание одного звена к другому. Финский профиль обеспечивает большую защиту от ветра и холода. Усадка с таким профилем происходит более равномерно и утеплитель если используется, то его практически не видно.

Структура материала

Весь подобный пиломатериал по своей структуре делится на виды:

1. Из цельного массива дерева.
2. Клееный профилированный.
3. Теплый брус.

Цельный профилированный брус изготавливают из массива дерева сечением 160-200, 200-200 мм. Все четыре стороны проходят обработку на специализированных станках. В итоге получается профилированный материал нужного сечения и вида профиля. Обычно при его изготовлении используют сорта хвойных деревьев.

Клееный профилированный товар изготавливают не только из хвойной древесины, но и из дуба. Конструкция такого материала состоит из досок – ламелей. Их склеивают между собой специальным клеем, укладывая каждую ламель противоположно сечению волокон предыдущей. Это делает такой вид сырья более прочным и придает ему устойчивость к возгоранию и гниению.

При изготовлении клееного товара доски проходят специальную отборку, что дает возможность улучшить ее эстетические свойства.

Отдельно хочется остановиться на таком новом виде этого бруса как «Теплый брус».

Теплый брус

[ads1]Новинка на строительном рынке, появился совсем недавно – это теплый пиломатериал. Он по своей структуре напоминает клееный, но обладает повышенной теплоизоляцией. Толщина строения из теплого бруса в 16 см, будет ровна стене из клееного в 37 см, а оцилиндрованного бревна в 47 см. Этот брус был разработан для строения и проживания в крайне жестких условиях. Например, на Севере. Такому дому будет не страшна температура в -50 градусов. Стоимость такого материала в разы меньше чем клееного.

Изготавливают его многослойно, используя слои ламелей и экструдированный пенополистирол. Склейка происходит под большим давлением и ламели используют только сухие.

Думаем, что этот товар займет достойное место в деревянном домостроении.

Внешний вид

Этот брус может отличаться по своему внешнему виду лицевой стороны. Существуют виды:

1. Прямолинейная внешняя сторона.
2. D – Образная лицевая сторона.

Прямолинейная внешняя сторона профилированного пиломатериала это стандартный вариант. Применяя такой вид, вы получите ровные и прямые внешние стены.

D – Образная лицевая сторона применяется для строений «Блок-Хаус». Этот вид бруса подходит тем, кто хочет иметь эстетический дом напоминающий русскую избу из бревна. Округлая внешняя сторона такого профилированного бруса даст возможность создать такое строение. При этом внутренние стены будут ровными.

Влажность материала

Профилированный продукт по степени влажности делится на два вида:

1. Профилированный брус естественной влажности.
2. Сушеный брус.

Материал естественной влажности будет содержать 20-25% влаги. Это пагубно сказывается на доме. Строения из материала естественной влажности будут давать усадку на 10%, но цена на такой профилированный брус будет меньше.

Сушеный профилированный брус проходит обработку в специальных камерах. Там его просушивают до влажности 8-12%. Такой материал не даст сильной усадки и меньше растрескается. Это дает возможность заселиться в дом сразу после строительства. Усадка такого дома будет составлять 3-5%. Стоит такой брус будет дороже, но разница сравняется. Так как после усадки брус естественной влажности высохнет и сильно растрескается, кроме того будет нужна дополнительная конопатка стен.

Дома из такого бруса во всей Европе считают домами Premium класса, так же как щитовые дома – эконом. Какой вид профилированного бруса выберете вы, зависит в конечном итоге только от вас.

Профилированный брус, виды профилей бруса, рамзеры, плюсы и минусы.

Профилированный брус это современный строительный материал который изготавливают из хвойных пород деревьев методом фрезерования и строгания. При этом, придаётся специальный профиль, такой материал легко укладывать, благодаря шипам-пазам, стены из него собираются, как конструктор, что существенно экономит время и деньги, стены при этом остаются геометрически ровными, благодаря жёсткому сцеплению, в виде замка и не требуют дальнейшей отделки.

Виды профилей и размеры

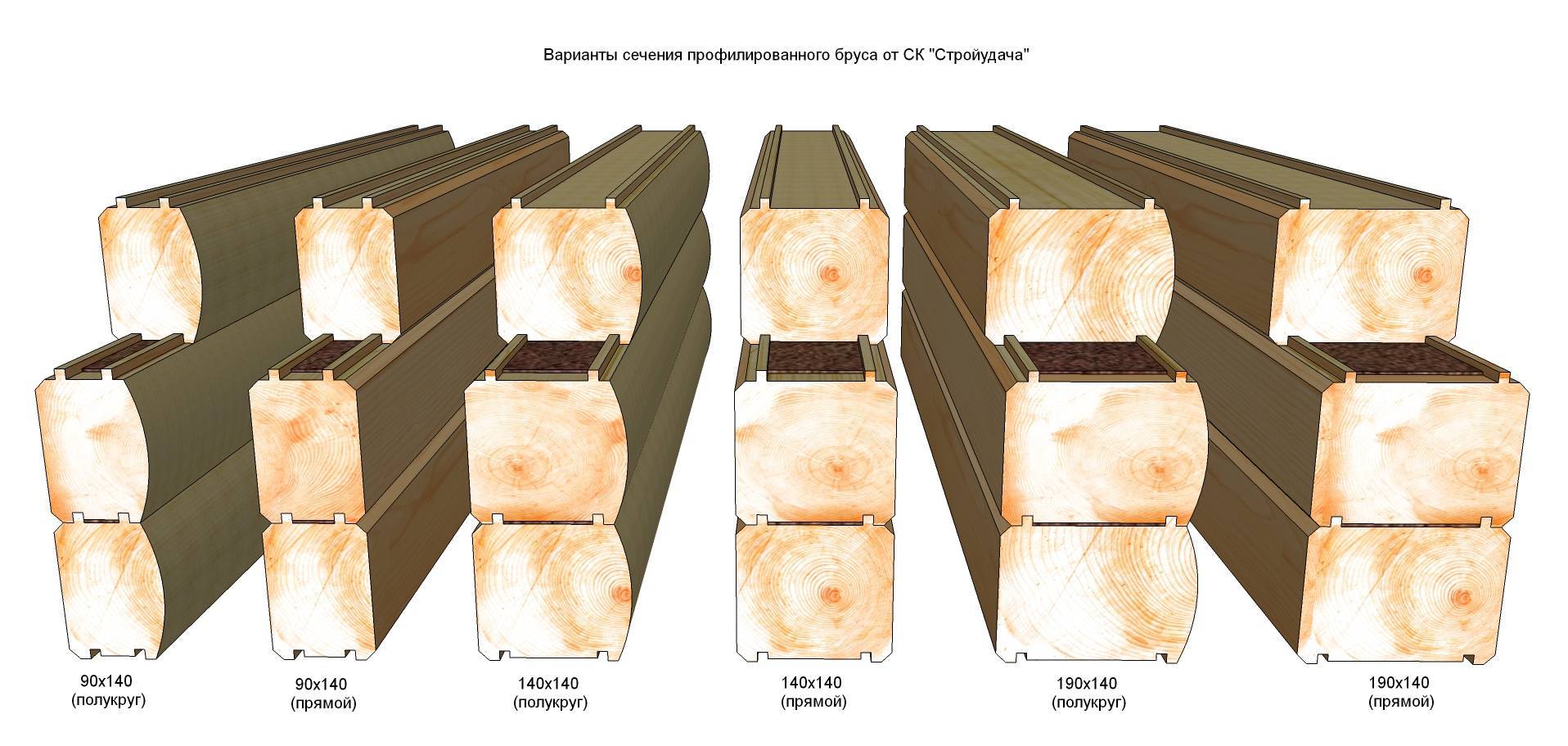
Существует три основных размера профилированного бруса: (размеры указаны в чистоте)

• 140 на 90 мм (толщина стены 9 см.)  — для дачных построек и главным образом идёт, как перегородчный брус
• 140 на 140 мм (толщина стены 14 см.) наиболее востребованный размер бруса, так называемая «золотая середина»
• 140 на 190 мм (толщина стены 19 см.) применяют для коттеджей и домов для постоянного проживания

По виду профиля:

• Финский — профиль бруса имеет два выраженных шипа
• Гребёнка — имеет большое количество шипов
• Скандинавский — это подвид, гребенчатого профиля.
• Лунный — или по другому под «блок хаус», полукруглый снаружи и ровный внутри, самый популярный вид бруса
• Ровный — профиль с двух сторон ровный, со скошенными фасками.

По степени влажности:

• Брус естественной влажности (25-40%)
• Брус камерной сушки(принудительной) (не более 20%)

По сезону заготовки:

• Зимний лес (сырьё для бруса, заготавливают зимой)
• Летний лес

Технология производства

Для производство профилированного бруса применяют хвойные породы дерева, ель или сосну. Берут заготовки не строганного бруса размерами 150 на 100, 150 на 150 или 150 на 200мм, в зависимости от размера, который хотим получить. Методом фрезерования, снимается с двух сторон по 0,5 см, при этом брусу задаётся профиль (полукруг с одной стороны или ровные бока, два шипа или гребёнка), в двух других формируют профиль в виде «шип-паз» На выходе мы получаем строганный профилированный с 4 сторон брус, весь процесс занимает 1-2 минуты на 1 шт. (брус длинной 6,0 метра). Профилирование производится на специальных четырёхсторонних строгальных станках профильными фрезами.

На фото стандартные заготовки не строганного бруса, готового для фрезерования и профилирования

Брус после профилирования в штабелях, готовый к отгрузке на пилораме

Крупным планом, профиль бруса снаружи под «блок хаус»( лунный)

Профиль бруса с двух сторон ровный естественной влажности под навесом перед отгрузкой

Важно: Чистовые стены из такого бруса обязательно нужно запиливать и врубать в коренной шип (другое название «тёплый угол») или в его разновидность, ласточкин хвост. Между венцами всегда прокладывают межвенцовый утеплитель джут.

Рубка углов домов, только в коренной шип, согласно ГОСТ 30974−2002

Утеплитель джут между каждым венцов бруса капитальных стен и перегородок

Благодаря шипам-пазам, брус соединяется в жёсткую геометрически ровную конструкцию

Для справки:

В одном кубе бруса 150 на 100мм — 11 шт.

В одном кубе бруса 150 на 150мм — 7,0 шт.

В одном кубе бруса 150 на 200мм — 5,5 шт.

Это влияет на стоимость сруба дома, к примеру дом равный по размеру и площади из бруса 150 на 200мм будет всегда дороже. Так как количество брусин в кубе меньше, а значит кубов для строительства нужно больше, учитывайте это при запросе или планирование строительства будущего дома

Выбор профиля бруса на стоимость не влияет (вы можете выбрать как  лунный профиль (под «блок хаус» снаружи) так и с двух сторон ровный).

• У нас собственное производство профилированного бруса.
• На производстве две сушильные камеры, к вашим услугам, брус камерной сушки.
• А так же лес, зимней заготовки.

SP932U Камера для профилирования луча | Ophir Photonics. на 4-м Международном семинаре по характеристике лазеров и оптики в Мюнхене, Германия. Эта статья основана на работе, выполненной в Spiricon в середине 90-х годов.

В то время были представлены новые идеи о том, как охарактеризовать лазерный луч. Предыдущие определения были несколько упрощенными и чаще всего объяснялись тем, что клиенты сообщали нам, как они хотят измерять луч.&nbspЧитать дальше…

Обеспечение качества сварных швов в медицинских устройствах

Многие клиенты, занимающиеся лазерной сваркой, измеряют мощность импульса своих лазеров, но все ли это данные, необходимые для обеспечения качества сварных швов? У Стива Шелленберга из Spinal Modulation были сомнения. Хотя он нашел измерение энергии импульса с помощью своего оборудования Ophir полезным для оценки своего процесса лазерной сварки, две его станции лазерной сварки производили сварные швы разного качества, несмотря на то, что они производили лазерные импульсы одинаковой энергии. Один лазерный сварщик, казалось, делал работу нормально, в то время как другой сварщик производил сварные швы значительно более низкого качества. Стив подозревал другой лазер&nbspЧитать далее. ..

Почему испытательное оборудование всегда вызывает подозрения?

Когда начинаются сбои в работе лазера и начинается диагностика, почему контрольно-измерительное оборудование в первую очередь подвергается сомнению в отношении точности, если первым вышел из строя лазер?&nbspПодробнее… анализ пучка во времени

Здесь мы показываем, что бесконтактное профилирование пучка на основе рэлеевского рассеяния полностью соответствует стандарту ISO11146&nbspПодробнее…

Отображение УФ-излучения с помощью ПЗС-камер

Можно ли получить изображение УФ-лазера с помощью ПЗС-камеры с кремниевым датчиком, предлагаемой Ophir-Spiricon? Ответ положительный, но прямой ультрафиолетовый свет со временем разрушает кремниевые ПЗС-чипы. Абляция является кумулятивной и зависит от интенсивности, длины волны и продолжительности воздействия света на датчик. Лучший выбор для визуализации УФ-излучения без повреждений — это избегать прямой визуализации луча на ПЗС-датчике с помощью преобразователя УФ-изображения. ..&nbspПодробнее…

Понимание динамического диапазона… Игра с числами

Существует значительная путаница, вызванная отчетами о динамическом диапазоне профилировщиков луча. Цель этого руководства по применению состоит в том, чтобы объяснить некоторые термины, используемые при обсуждении этого параметра как компанией Ophir-Spiricon, так и другими поставщиками профилировщиков луча. ОпределениеДинамический диапазон — это отношение самого большого измеримого сигнала к наименьшему измеримому сигналу. Наименьший измеримый сигнал обычно определяется как сигнал, равный уровню шума, или, в качестве альтернативы, «эквивалентная экспозиция шума» или точка, в которой отношение сигнал/шум (SNR) равно 1. Чтобы&nbspЧитать дальше…

Метод измерения расходимости фокусного расстояния

Метод измерения расходимости фокусного расстояния основан на ширине луча размера пятна сфокусированного луча и фокусном расстоянии фокусирующей оптики. Метод расходимости фокусного расстояния позволяет определить расходимость луча в дальней зоне в любой точке пути распространения луча. Как показано ниже, расчет, выполняемый программой BeamGage®, довольно прост; однако оптическая настройка должна быть выполнена с большой осторожностью.&nbspПодробнее…

Словарь измерений лазерного луча

Длина волны : В физике длина волны синусоидальной волны — это пространственный период волны — расстояние, на котором форма волны повторяется[1], и величина, обратная пространственной частоте. Обычно он определяется путем рассмотрения расстояния между последовательными соответствующими точками одной и той же фазы, такими как гребни, впадины или пересечения нуля, и является характеристикой как бегущих, так и стоячих волн, а также других пространственных волновых моделей. 3] Длину волны обычно обозначают греческой буквой лямбда (λ)…&nbspПодробнее…

Информационный документ – Точность измерения ширины луча

Введение&nbspПодробнее…

Информационный документ – От яблока к яблоку: какие технологии камер лучше всего подходят для приложений профилирования луча, Часть 2: Базовые методы и эффекты режимов

Автор G.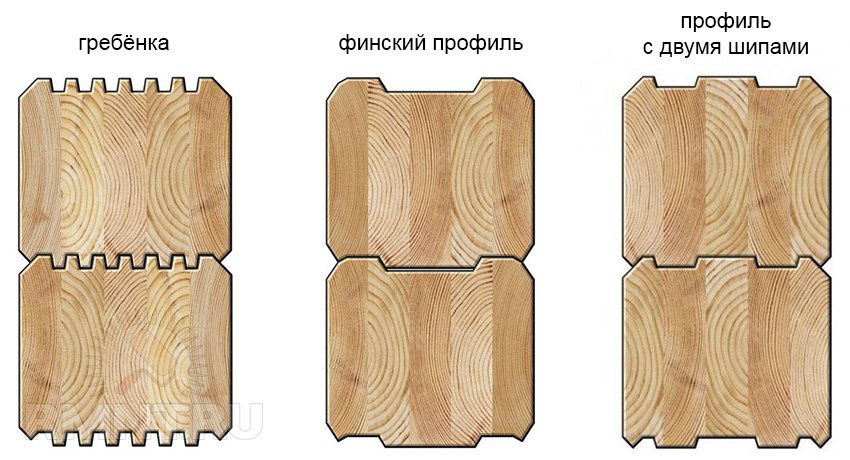 E. Слободзян, технический директор, на пенсии, Ophir-Spiricon&nbspПодробнее…

Профилирование BeamGage с интерфейсом автоматизации .Net и LabVIEW®

BeamGage Professional и BeamGage Enterprise версии 5.7 поддерживаются с помощью компонентов автоматизации .Net. Оба включают пример LabVIEW, который можно запустить с помощью механизма LabVIEW Run-Time Engine, который поставляется на компакт-диске с программным обеспечением BeamGage или доступен для бесплатной загрузки с сайта National Instruments.&nbspПодробнее…

Медицинские лазеры: Когда применение лазера требует максимальной безопасности

Непрерывное развитие лазерных технологий за последние десятилетия произвело революцию во многих областях нашей жизни. Наиболее непосредственное влияние на человека оказывают достижения в области лазерных технологий для медицинских или косметических целей. Если вы хотите обеспечить оптимальные результаты, вы должны знать и измерять критические параметры лазера.&nbspПодробнее. ..

Формирование рентгеновского луча с помощью деформируемых зеркал: расчет профиля поверхности и функции рассеяния точки для гауссовых лучей с использованием физической оптики

• Список журналов
• J Синхротронное излучение
• PMC5741128

Являясь библиотекой, NLM предоставляет доступ к научной литературе. Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.

Узнайте больше о нашем отказе от ответственности.

J Синхротронное излучение. 2018 1 января; 25 (часть 1): 123–130.

Опубликовано в Интернете 1 января 2018 г. doi: 10.1107/S1600577517014035

Информация об авторе Примечания к статье Информация об авторских правах и лицензии Отказ от ответственности медицинские изображения и лучи синхротронного лазера / лазера на свободных электронах. В то время как деформации профиля зеркала могут привести к ухудшению резкости фокуса, можно произвести преднамеренную деформацию зеркала, чтобы придать фокусу желаемый размер и распределение, через пьезоактуаторы . Результирующий профиль можно охарактеризовать с помощью подходящих метрологических инструментов и сопоставить с ожидаемым оптическим качеством через код распространения волнового фронта или, иногда, спрогнозировать с помощью геометрической оптики. В последнем случае и для специального класса деформаций профиля с монотонно возрастающей производной , т.е. вогнутой вверх, функция рассеяния точки (ФРТ) может быть предсказана даже аналитически. Более того, при этих предположениях соотношение может быть и обратным: по желаемой ФРТ требуемую деформацию профиля можно вычислить аналитически, избегая использования поисковых кодов методом проб и ошибок. Однако расчет пока ограничивался геометрической оптикой, что влекло за собой некоторые ограничения: например, не учитывались эффекты зеркальной дифракции и размер источника когерентного рентгеновского излучения. В этой статье рассматривается формализм формирования луча в рамках физической оптики в пределе малых длин волн света и в случае гауссовых волновых фронтов интенсивности. Также показаны некоторые примеры сформированных профилей, направленных на преобразование гауссовского распределения интенсивности в цилиндрическое, и проверки характеристик формирования, вычисляющих PSF на длине волны с помощью Код WISE сделан.

Ключевые слова: Рентгеновские зеркала, активная оптика, формирование луча, физическая оптика

В последние годы были предприняты большие усилия для производства рентгеновских зеркал с высокой разрешающей астрономия и наземные средства, такие как синхротроны и лазеры на свободных электронах (ЛСЭ). Разрешающая способность — это размер фокального пятна, обычно выражаемый через функцию рассеяния точки (PSF). Форма PSF представляет собой комбинацию дифракции на собственной апертуре и дефектов изготовления зеркала, которые, в свою очередь, включают геометрические деформации и дефекты отделки поверхности.

Угловое разрешение в астрономических рентгеновских телескопах (VanSpeybroeck & Chase, 1972 ▸), т. е. способность разделять отдельные источники в переполненных полях, в настоящее время колеблется от 0,5   угловой секунды для рентгеновской обсерватории Чандра (Weisskopf, 2012 ▸ ) до 16   угловой секунды для eROSITA (Burwitz et al. , 2013 ▸; будет запущен в 2018 году). Различная стоимость связана с различной технологией производства, прямой формовкой/полировкой толстых зеркал для Chandra и гальванопластикой никеля тонких корпусов зеркал для eROSITA. Конструкция оптической системы на основе тонких зеркальных оболочек удобна, в частности, для получения больших площадей сбора, так как позволяет плотную вложенность ряда оболочек, что позволяет обнаруживать далекие и слабые источники рентгеновского излучения. Тем не менее, тонкие оболочки зеркал более подвержены деформациям, и поэтому более высокая плотность вложенности всегда достигается за счет точности фокусировки, которая на сегодняшний день остается ограниченной дефектами профиля и поверхности.

Оптические системы для наземных источников рентгеновского излучения обычно фокусируют, коллимируют и отклоняют интенсивные рентгеновские лучи; поэтому эти зеркала не требуют большой эффективной площади. Вложение также не требуется, поэтому зеркала в оптической установке могут быть толстыми, чтобы максимизировать их механическую жесткость. Следовательно, могут быть предприняты усилия, направленные на наилучшую возможную отделку поверхности и достижение зеркального профиля, максимально близкого к номинальному: , например. эллипсоид или система К-Б (Вольтер, 19 лет).52 ▸; Киркпатрик и Баэз, 1948 ▸). Достигаемая точность профиля может быть настолько высокой, что ФРТ становится ограниченной деформацией, вызванной несущей системой или нестабильностью температуры, и поэтому форму зеркала приходится активно корректировать во время эксплуатации. Этого можно добиться, снабдив зеркало системой изгибов (Raimondi и др. , 2014 ▸) для общей коррекции кривизны или биморфными приводами для достижения коррекции в более коротких пространственных масштабах (Signorato и др. , 1998 ▸). В лучших случаях, с фокусным пятном в несколько нанометров, эта оптика в настоящее время приближается к пределу дифракции в мягком рентгеновском излучении (Idir et al. , 2010 ▸). На практике существуют практические ограничения поправок, которые могут выполняться с помощью приводов , такие как максимальное напряжение, которое они могут оказывать на зеркала, сложность моделирования поверхности на стыках между приводами и реалистичное определение напряжений для применяться (Ваннони и др. , 2015 ▸).

Однако для некоторых приложений максимальная резкость сфокусированного луча не требуется. Скорее, продольному профилю зеркала можно придать преднамеренную деформацию, чтобы перераспределить мощность, перехватываемую зеркалом, и придать ФРТ заданный профиль. Возможности формирования луча имеются, например, на линии луча EIS-TIMEX FERMI (Светина и др. , 2012 ▸), где изначально гауссово распределение интенсивности превращается в цилиндрическую ФРТ в фокальной плоскости. Однако форма зеркала была найдена методом проб и ошибок, и поиск нужно будет повторять каждый раз при изменении требуемого профиля PSF. Напротив, аналитический инструмент, способный вернуть изгиб зеркала для любой требуемой PSF, был бы намного более эффективным и простым в реализации.

В то время как проблема вычисления ФРТ, генерируемого возмущенным профилем зеркала, широко изучается, например. с использованием специальных процедур трассировки лучей, обратная задача требует гораздо более деликатного решения. Этот момент показан на рис. 1: если это профиль зеркала, который точно фокусирует падающий луч ( например, эллипс для наземных источников, парабола для бесконечно удаленного источника), мы можем изменить этот профиль, добавив небольшое возмущение, направленное на изменение распределения интенсивности по ФРТ. Если можно использовать геометрическую оптику, PSF можно вычислить по возмущенному профилю =  + , и это будет только функция распределения углов падения вдоль х . Однако, если наклоны достаточно малы, изменение угла падения можно аппроксимировать с помощью  + . Поскольку по гипотезе возвращается идеальный фокус, PSF должна быть функцией единственного, , т. е. , «ошибки профиля». Аналогичный аргумент, основанный на физической оптике, можно использовать, чтобы прийти к такому же выводу (Raimondi & Spiga, 2015 ▸). Ясно, что не существует уникального зеркала, которое возвращает назначенный PSF; скорее, бесконечное количество возможных ошибок профиля может быть связано с определенной формой PSF.

Открыть в отдельном окне

( a ) Номинальный продольный профиль зеркала точно фокусирует падающий луч в точку фокусировки. ( b ) Преднамеренная деформация наложена, чтобы изменить распределение интенсивности в фокальной плоскости. Продольный профиль теперь = + .

К счастью, для настоящего объема формирования луча нам нужно получить только одиночное
функция для получения выбранного PSF. В частности, можно выбрать зеркальный профиль с самыми простыми свойствами, напр. без изменений вогнутости. Основываясь на этой гипотезе и предполагая, что геометрическая оптика полностью применима, мы разработали одномерный формализм (Spiga et al. , 2013 a
▸) для вычисления деформации профиля по любой желаемой PSF и произвольному распределению интенсивности, падающей на зеркало. Ясно, что этот подход всегда возвращает непрерывных деформаций и не всегда может быть совместим с системой изгиба/биморфа, доступной для используемой оптической системы, обычно состоящей из дискретных элементов. Другие авторы (Laundy et al. , 2015 ▸; Sutter et al. , 2016 ▸) разработали методы для учета конечного размера исполнительных механизмов и максимально возможного воспроизведения цилиндрической PSF. Однако в оставшейся части этой статьи мы не рассматриваем это ограничение, а подходим к решению проблемы формирования луча, предполагая, что технология, позволяющая применять непрерывное распределение деформации вдоль профиля зеркала, станет доступной в ближайшее время. На практике настоящее рассмотрение применимо к очень большому набору очень маленьких исполнительных механизмов, таких как реализованный Рейдом 9.0085 и др.  (2014 ▸).

Наш расчет, основанный на геометрической оптике, не учитывал пространственную когерентность падающего волнового фронта, поэтому пренебрегали эффектами дифракции на апертуре, а также размерами источника. В этой статье мы перевыводим наши предыдущие результаты в рамках более общей трактовки физической оптики (§2), в частом случае малых значений λ и для гауссовых волновых фронтов интенсивности, типичных для ЛСЭ в основной моде распространения ( Раймонди и др. , 2013 ▸). Это не только позволяет нам понять, в каком приближении справедливы формулы формирования луча, но также дает возможность проверить реальные характеристики формирования луча с учетом когерентности падающего волнового фронта, который автоматически содержит всю информацию о профиле источника. С этой целью мы используем формализм одномерной дифракции Френеля (Spiga & Raimondi, 2014 ▸; Raimondi & Spiga, 2015 ▸), реализованный в WISE 9. Код 0086 ( Код имитации распространения волнового фронта ). Это описано в §3 вместе с некоторыми примерами вычислений.

2.1. Общее выражение PSF в условиях дальнего поля

Как указано в § 1, здесь предполагается, что номинальная форма зеркала точно фокусирует источник в начале системы отсчета, а возмущение, сообщаемое профилю зеркала, по-прежнему описывается формулой (рис. 1). Если волновой фронт имеет однородную амплитуду, ФРТ на длине волны света λ имеет выражение (Raimondi & Spiga, 2015 ▸) в приближении дальнего поля,

, где α — угол скользящего падения, λ — длина волны света, θ — угловое расстояние от центра идеального фокусного пятна, а ≃ — апертура зеркала в плоскости, перпендикулярной направлению луча. Мы предполагаем, что L , длина зеркала, много меньше, чем расстояние до плоскости наблюдения. Что касается выражения в оригинальной статье, мы изменили обозначение, заменив его на , потому что x теперь обозначает координату по длине зеркала, а не по входному зрачку.

Если волновой фронт неоднороден , т.е. характеризуется изменением интенсивности с x , выражение PSF легко адаптируется,

где — действительная функция, представляющая амплитуду электрического поля на поверхности зеркала, и предполагается нормализованным к 1 по интенсивности,

, включившим в определение постоянную зеркальную отражательную способность. Единицы равны , и по этой причине L появляется в первой степени в уравнении (2). Выражение {…} в уравнении (2) известно как комплексная функция зрачка (CPF).

Теперь мы расширим диапазон интегрирования до , установив значение равным нулю за пределами длины зеркала. Затем мы применяем теорему Винера-Хинчина к уравнению (2) и удаляем модуль в квадрате,

, где второй интеграл — автокорреляционная функция CPF, а h — «запаздывание» между амплитудным профилем и его сдвинутой копией . Переставив члены, мы можем переписать уравнение (4) в виде

Мы не включаем ни в какую шероховатость ( т. е. фрактальную) составляющую, поэтому профиль везде имеет производную и можно записать = , при . Таким образом, мы получаем

2.2. Случай гауссова пучка при малых λ

Ограничимся теперь случаем гауссова анизотропного пучка, т.е.

где нормировочный коэффициент выбран для выполнения уравнения (3), а среднеквадратичное значение ширины амплитуды. в месте расположения зеркала, измеренного в плоскости, поперечной направлению распространения. Гауссова теория распространения луча показывает, что ≃ , где – среднеквадратичное значение ширины источника. D – расстояние зеркало–источник (Раймонди и др. , 2013 ▸). Подставив выражение в уравнение (6) и поменяв порядок интегрирования, получим

где мы подставили = . Мы дополнительно предполагаем, что для рентгеновских лучей длина волны намного меньше, чем длина когерентности поверхности, , т.е. .
1, и поэтому только небольшой интервал ≃ 0 дает вклад в интеграл. Следовательно, мы можем написать ≃ . Если мы теперь установим = , уравнение (8) будет выглядеть как

Изменяя переменную интегрирования во втором интеграле, после некоторой обработки мы остаемся с

и интеграл в явно равен , так что мы получаем

В случае идеального зеркала, = 0, = и уравнение (11) дает

что после некоторых простых переходов возвращает

Как и ожидалось, когерентное распространение гауссового волнового фронта вернул изображение, воспроизводящее профиль источника, т.е. с той же характерной шириной = . В общем случае интеграл в уравнении (11) не может быть решен аналитически, поскольку зависит от функционального вида .

2.3. Формулы формирования пучка в геометрическом оптическом пределе

Путем некоторых манипуляций уравнение (11) можно представить в виде Мы остаемся с

, где мы использовали соотношение = . Второй фактор в интеграле — это просто профиль амплитуды источника, видимого на расстоянии 90 085 D 90 086 и «искаженного» возмущением профиля. Уравнение (15) уже не зависит от λ, поэтому сделанное нами приближение есть переход к геометрической оптике. Отметим также, что в пределе точечного источника профиль источника становится дельта-функцией Дирака, и уравнение (15) принимает более простой вид

, который просто представляет собой перераспределение интенсивности волнового фронта в соответствии с функцией = .

Теперь воспользуемся дополнительной гипотезой о том, что
будет возрастающей функцией x . Это означает, что функция = может быть инвертирована, поэтому мы можем изменить переменную интегрирования на м в уравнении (15),

, где м варьируется между минимальным = и максимальным значением = .

Наконец, в пределе точечного источника гауссовский член в уравнении (17) становится дельтой, и результат становится равным

для всех значений θ, которые соответствуют примерно x
через уравнение

, которое устанавливает однозначное соответствие между положением на профиле зеркала, x , и угловой координатой PSF, θ. Это именно то выражение PSF, которое мы уже получили (Spiga et al. , 2013 a
▸) через чисто геометрическое рассуждение. Этот подход, основанный на обнаружении кривизны, был также распространен на внутрифокальную конфигурацию для восстановления формы зеркала при рентгеновском освещении (Spiga 9).0085 и др. , 2013 б
▸).

Монотонный тренд явно подразумевает, что 0 по всей длине зеркала. В местах, где = 0, PSF демонстрирует либо каспы, либо дираковские дельта-подобные пики, в зависимости от того, исчезает ли она либо в изолированных точках, либо в зеркальных сегментах [см. Spiga et al. (2013 и
▸) для получения дополнительной информации]. В любом случае ФРТ, обеспечиваемая уравнением (18), нормирована,

Используя уравнение (19), мы можем переписать уравнение (18) следующим образом,

и решение этого уравнения

Справедливость уравнений (18) и (22) не ограничивается случаем гауссовых волновых фронтов. Теперь мы можем заменить любые две функциональные формы для PSF(θ) и – неотрицательные и удовлетворяющие условиям нормировки (3) и (20) – в уравнение (22) и решить его относительно . При этом могут возникнуть проблемы, когда = 0 в одном или нескольких интервалах профиля зеркала или если ФРТ равна нулю в какой-то области фокальной плоскости (как в примере, показанном на рис. 6). К счастью, с этими особыми случаями можно легко справиться: подробное обсуждение этих тем сообщает Spiga 9.0085 и др. (2013 и
▸).

Наконец, мы замечаем, что представленная здесь трактовка справедлива в том пределе, когда расстояние до плоскости наблюдения много больше, чем L . Если это условие нарушается, мы можем учесть конечное фокусное расстояние, корректирующие уравнения (18)–(22), с соответствующим коэффициентом асимметрии. Опять же, подробное обсуждение этой темы можно найти в Spiga et al. (2013 и
▸).

Теперь рассмотрим несколько примеров применения формул формирования луча, описанных в предыдущем разделе. Сначала мы рассматриваем наиболее часто запрашиваемую форму PSF, т. е. цилиндрический,

Заменяя теперь выражения [уравнение (7)] и цилиндрического PSF в уравнение (22) и решая численно для различных значений ω, мы получаем различные профили, как показано на рис. 2( a ), всегда нацеливаясь на один и тот же цилиндр PSF (рис. 2 b
).

Открыть в отдельном окне

( a ) Сплошные линии: деформации профиля, необходимые для превращения гауссовых амплитудных распределений (штриховые линии) переменной ω [уравнение (7)] в ту же цилиндрическую ФРТ, показанную на ( б ). Мы приняли значения L = 400 мм, α = 1° и уравнение (23) с w = 4 мкрад; графики гауссовых амплитуд имеют произвольные единицы измерения.

Теперь мы можем проверить эффективность фасонных профилей, используя уравнение (1), реализованное в коде WISE (Raimondi & Spiga, 2015 ▸). В этих симуляциях мы наложили возмущения, показанные на рис. 2 ( a ), на эллиптическое зеркало с сагиттальным радиусом кривизны = 1165  мм, расстояние f = 40 м до фокальной плоскости и расстояние D = 200 м до источника света. Угол падения α = 1°. ФРТ рассчитаны при λ = 30 Å на рис. 3 и при λ = 10 Å на рис. 4. Мы сразу отмечаем, что моделирование физической оптики отклоняется от целевого ФРТ, потому что края не являются резкими, а также из-за наличия дифракционных полос. переменной амплитуды и частоты. Наилучшее приближение к цилиндрическому профилю явно получается при более высокой энергии с более широким лучом (случай ω = 2  мм на рис. 4). Это соответствует нашим выводам из § 2.3 о том, что результаты геометрической оптики достигаются в пределах малых λ и . Наименьшие значения, соответствующие большим отверстиям луча на зеркале, вызывают меньшие отклонения от геометрической оптики, поскольку луч дифрагирует через более широкую «щель» (примерно широкую). Обратное происходит при больших значениях λ и , соответствующих дифракции на малом 2ω. Это видно, например, на рис. 5, где мы отобразили эволюцию ФРТ для гипотетически фиксированного значения ω = 1 мм и переменной длины волны рентгеновского излучения: в случае λ = 30 Å цилиндрический профиль полностью скрыт гауссов профиль источника. Таким образом, используя метод физической оптики для расчета ФРТ, нам даже не нужно сворачивать ФРТ с уменьшенным профилем источника, потому что вся информация о размере источника уже включена в ширину фронта гауссовой волны на зеркале. Это возможно, потому что предполагается, что волновой фронт обладает высокой пространственной когерентностью, что типично для ЛСЭ и большинства каналов синхротронного излучения.

Открыть в отдельном окне

WISE моделирование ФРТ для возмущений профиля, показанных на рис. 2, при λ = 30 Å при переменных значениях ω. Характерная ширина гауссового источника равна 0,48, 0,96 и 1,92 мкрад в трех случаях соответственно.

Открыть в отдельном окне

WISE моделирование ФРТ для возмущений профиля, показанных на рис. 2, при λ = 10 Å при переменных значениях ω. Характерная ширина гауссового источника равна 0,16, 0,32 и 0,64 мкрад в трех случаях соответственно.

Открыть в отдельном окне

WISE моделирование ФРТ для возмущения профиля, показанного на рис. 2, в случае ω = 1 мм при уменьшении значений λ. Характерная ширина источника Гаусса составляет 0,96, 0,32 и 0,03 мкрад для трех длин волн соответственно.

До сих пор мы рассматривали случай цилиндрической ФРТ, но метод, изложенный в этой статье, одинаково работает для любых неотрицательных и нормализованных ФРТ. Например, ФРТ, показанная на рис. 6( b ), состоящий из трех отдельных пиков, можно легко воспроизвести – из гауссовых волновых фронтов на зеркале – путем придания деформации, как показано на рис. 6 ( a ): и в этом случае форма профиля была адаптирована к фактическая ширина гауссова луча, чтобы всегда возвращать один и тот же ФРТ. В этом случае решение уравнения (22) может вызвать некоторые проблемы, поскольку левая часть становится постоянной в соответствии с зазорами ФРТ, и, следовательно, возможны бесконечные значения . Эту проблему можно решить, приняв за предельное значение ближайшую границу интервалов, где левая часть уравнения (22) постоянна. Обычно это приводит к разрывам и, следовательно, к перегибам, как показано на рис. 6(9).0085 и ).

Открыть в отдельном окне

( a ) Сплошные линии: деформации профиля, необходимые для превращения гауссовых амплитудных распределений (штриховые линии) переменной ω [уравнение (7)] в одну и ту же ФРТ ( b ), состоящую из трех отдельных блоков. Как и при моделировании PSF цилиндра, мы использовали значения L = 400 мм, α = 1°, а графики гауссовой амплитуды имеют произвольные единицы. Полный диапазон профилей не показан, чтобы привлечь внимание к фигурному центру, где имеет значение интенсивность луча: опущенные части соответствуют хвостам гауссовой диаграммы и просто состоят из прямых (неформирующих) сегментов. Стрелками отмечены перегибы профиля, необходимые для создания зазоров в PSF.

Также с этой деформацией профиля мы проверили реальную PSF, используя код WISE для различных длин волн рентгеновского излучения (рис. 7 и 8), ограничиваясь случаем, в котором мы ожидаем минимизировать дифракционные эффекты, т.е. ω = 2 мм. В действительности дифракционные особенности в этом примере даже более очевидны, чем в рассмотренном ранее цилиндрическом профиле, потому что пик ФРТ больше направлен к центру. При моделировании (рис. 7) при 30   Å три пика кажутся смешанными в одном, поскольку угловой диаметр источника составляет порядка 1 мкрад, что близко к размеру зазоров (2 мкрад), ожидаемому геометрически. При 10 Å начали проявляться структуры отдельных пиков (рис. 7), но они все еще частично скрыты заметными дифракционными полосами. При более высоких энергиях (рис. 8) полосы все еще присутствуют, но общая ФРТ теперь лучше соответствует ожидаемому профилю ФРТ, а промежутки между тремя блоками теперь лучше видны. Наконец, при λ = 0,3 Å геометрическая картина хорошо воспроизводится при моделировании (рис. 8), даже если некоторые краевые эффекты все еще можно увидеть. Таким образом, мы можем утверждать, что для ФРТ такого типа и гауссова пучка такой ширины характеристики детерминированного метода формирования пучка удовлетворительны при энергиях выше 40 кэВ.

Открыть в отдельном окне

WISE моделирование ФРТ для возмущения профиля, показанного на рис. 6 ( a ), в случае ω = 2  мм при двух разных значениях λ. Характерная ширина гауссового источника равна 0,48 и 0,16 мкрад в обоих случаях соответственно. Моделирование при двух меньших значениях λ включено в рис. 8, чтобы избежать путаницы на рисунке.

Открыть в отдельном окне

WISE моделирование ФРТ для возмущения профиля, показанного на рис. 6( a ) в случае ω = 2 мм, при двух значениях λ меньше используемых на рис. 7. Характерная ширина гауссового источника равна 0,08 и 0,005 мкрад в двух случаях соответственно.

В этой статье мы представили полный вывод аналитических формул [уравнения (18) и (22)] для детерминированного формирования луча когерентных гауссовских волновых фронтов, исходя из физических оптических выражений ФРТ, в пределе малых длин волн и малых источников рентгеновского излучения. Метод ограничен непрерывными деформациями профиля и не учитывает дискретность приводов, которые в современной пьезотехнологии можно использовать для активной коррекции формы деформируемых зеркал. Однако аналитический метод позволяет избежать сложных алгоритмов поиска и возвращает при достаточно высоких энергиях рентгеновского излучения ФРТ, очень близкую к требуемой, в чем мы легко могли убедиться с помощью Код WISE . Таким образом, этот подход может эффективно обеспечить первоначальную коррекцию профиля для последующего уточнения с помощью численных алгоритмов для учета упомянутых ограничений (конечные размеры источника и пьезоэлементов). Дальнейшая работа будет направлена ​​на поиск более общих формул для описания формализма формирования луча на используемой длине волны без необходимости перехода к пределу геометрической оптики.

• Бурвитц В., Предель П., Браунингер Х., Буркерт В., Деннерл К., Эдер Дж., Фридрих П., Фюрмец М., Гризони Г., Хартнер, Г., Мариони Ф., Менц Б., Пфефферманн Э. и Вальсекки Г. (2013). Проц. SPIE , 8861 , 88610J.
• Идир, М., Мерсер, П., Моди, М. Х., Довиллер, Г., Левек, X., Букур, С., Эсколано, Л. и Соважо, П. (2010). Нукл. Инструм. Методы физ. Рез. А , 616 , 162–171.
• Киркпатрик П. и Баэз А. (1948). J. Опт. соц. Являюсь.
  38 , 766–774. [PubMed]
• Лаунди, Д., Алианелли, Л., Саттер, Дж., Эванс, Г. и Сони, К. (2015). Опц. Экспресс , 23 , 1576–1584. [PubMed]
• Раймонди, Л. и Спига, Д. (2015). Астрон. Астрофиз.
  573 , А22.
• Раймонди Л., Светина К., Мане Н., Кокко Д., Абрами А., Де Марко М., Фава К., Герусина С., Гобесси Р., Капотонди, Ф., Педерсоли Э., Кискинова М., Де Нинно Г., Зейтун П., Довиллер Г., Ламбер Г., Буту В., Мерджи Х., Гонсалес А. И., Готье, Д. и Занграндо, М. (2013). Нукл. Инструм. Методы физ. Рез. А , 710 , 131–138.
• Раймонди Л., Светина К., Мане Н., Кокко Д., Капотонди Ф., Педерсоли Э., Манфредда М., Кискинова М., Кейтель Б., Бреннер Г. ., Пленьес, Э., Мей, Т., Манн, К. и Занграндо, М. (2014). Проц. SPIE , 9208 , 920804.
• Рейд, П. Б., Олдкрофт, Т. Л., Очарованный, Р., Котронео, В., Джонсон-Уилке, Р. Л., Маркес, В., Макмалдрох, С., О’Делл, С. Л. , Рэмзи Б.Д., Шварц Д.А., Тролиер-МакКинстри С.Е., Вихлинин А.А., Уилке Р.Х.Т. и Чжао Р. (2014). Проц. SPIE , 9208 , 920807.
• Синьорато Р., Хигнетт О. и Гулон Дж. (1998). J. Синхротронный рад.
  5 , 797–800. [PubMed]
• Spiga, D., Basso, S., Bavdaz, M., Burwitz, V., Civitani, M., Citterio, O., Ghigo, M., Hartner, G., Menz, B., Парески, Г., Просерпио, Л., Салмасо, Б., Тальяферри, Г., Вилле, Э. (2013 b ). Проц. SPIE , 8861 , 88611F.
• Спига, Д. и Раймонди, Л. (2014). Проц. SPIE , 9209 , 92090E.
• Спига Д., Раймонди Л., Светина К., Занграндо М. (2013 a ). Нукл. Инструм. Методы физ. Рез. A , 710 , 125.