Физические основы механики
Представим себе материальную точку, движущуюся по некоторой криволинейной траектории . Запишем скорость в виде
и заметим, что вектор
— это единичный вектор, касательный к траектории и совпадающий по направлению с вектором скорости. Продифференцируем вектор скорости, записанный в данном представлении, и получим
Мы представили ускорение в виде двух слагаемых. Заметим прежде всего, что слагаемые ортогональны друг другу. Действительно, поскольку вектор — единичный, то
Дифференцируя это скалярное произведение, получаем
то есть
по свойству скалярного произведения.
Таким образом, мы разложили ускорение на сумму двух взаимно ортогональных составляющих, обозначем их и :
Обсудим физический смысл каждого слагаемого. Слагаемое
— это тангенциальное ускорение, которое характеризует быстроту изменения модуля скорости. Эта часть полного ускорения направлена либо по скорости, когда производная dv/dt > 0, то есть движение ускоренное, либо в сторону противоположную скорости, когда эта производная dv/dt < 0, то есть движение замедленное. Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:
Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:
Слагаемое
направлено по нормали к траектории — перпендикулярно касательной к траектории и называется нормальным ускорением. Если тангенциальное ускорение определяет скорость, с которой меняется модуль вектора скорости, то нормальное ускорение определяет скорость, с которой меняется направление вектора скорости.
Рис. 2.10. К определению кривизны траектории
Рассмотрим «достаточно гладкую», в остальном произвольную плоскую криволинейную траекторию. Плоскую, то есть все точки траектории лежат в некоторой плоскости, — исключительно для упрощения выкладок, получаемый в рамках этого предположения, результат годится и для любой «достаточно гладкой» пространственной кривой, чьи точки уложить в одну плоскость невозможно. Последнее обстоятельство мы здесь рассматривать не будем, оно строго доказывается методами аналитической геометрии. Слова «достаточно гладкая» означают, что кривая описывается непрерывной функцией, имеющей непрерывные первую и вторую производные. С точки зрения физических приложений, требование существования непрерывных первых двух производных фактически не является ограничением на форму траектории, так как практически всегда выполнено. Проще говоря, на траектории не должно быть «углов» типа показанного на рисунке 2.11.
Слова «достаточно гладкая» означают, что кривая описывается непрерывной функцией, имеющей непрерывные первую и вторую производные. С точки зрения физических приложений, требование существования непрерывных первых двух производных фактически не является ограничением на форму траектории, так как практически всегда выполнено. Проще говоря, на траектории не должно быть «углов» типа показанного на рисунке 2.11.
Рис. 2.11.
Такую «гладкую» кривую на любом её бесконечно малом участке можно заменить (рис. 2.12) участком окружности некоторого радиуса. Радиус этой окружности, аппроксимирующей траекторию на её бесконечно малом участке в окрестности некоторой точки, принято называть радиусом кривизны траектории в этой точке. Центр этой окружности принято называть центром кривизны траектории в данной точке. Кривизной траектории называется величина C = 1/R. Подчеркнем, что радиус кривизны, как и центр кривизны траектории — её локальные характеристика: каждой точке траектории соответствует свой радиус кривизны и свой центр кривизны. Исключениями являются: 1) окружность, её радиус кривизны во всех её точках один и тот же и равен радиусу окружности, центр кривизны «один на всех» и совпадает с центром окружности, и 2) прямая, для любой точки прямой радиус кривизны бесконечен, а центр кривизны находится в бесконечно удаленной от прямой точке. Это легко понять: давайте увеличивать радиус окружности, чем больше радиус окружности, тем ближе любой её конечный участок к участку прямой. На равнине, лучше всего на пляже, с высоты человеческого роста до горизонта не более пяти километров, — в этих пределах Земля плоская.
Исключениями являются: 1) окружность, её радиус кривизны во всех её точках один и тот же и равен радиусу окружности, центр кривизны «один на всех» и совпадает с центром окружности, и 2) прямая, для любой точки прямой радиус кривизны бесконечен, а центр кривизны находится в бесконечно удаленной от прямой точке. Это легко понять: давайте увеличивать радиус окружности, чем больше радиус окружности, тем ближе любой её конечный участок к участку прямой. На равнине, лучше всего на пляже, с высоты человеческого роста до горизонта не более пяти километров, — в этих пределах Земля плоская.
Рис. 2.12. К определению радиуса кривизны траектории
Вычислим модуль производной , входящей в выражение для нормального ускорения. Направлен вектор по нормали к траектории к центру к центру кривизны, что поясняет рис. 2.13.
Рис. 2.13. Графическое определение радиуса кривизны траектории
Для этого прежде всего перейдем от дифференцирования по времени к дифференцированию по «пути»: , имеем:
По определению производная кривизне кривой C, а величина ей обратная равна радиусу кривизны кривой R. Собирая всё вместе, для нормального ускорения окончательно получаем:
Собирая всё вместе, для нормального ускорения окончательно получаем:
,
где нормаль перпендикулярна к касательной и всегда направлена к центру кривизны, см. рис. 11.
Приведем некоторое дополнительное пояснение к рисунку 11. Возьмем неподалеку от точки 1 точку 2. Построим в этих точках касательные единичные векторы 1 и 2. Перпендикуляры к этим касательным пересекутся в некоторой точке O2. Заметим, что для кривой, не являющейся окружностью, расстояния R1 и R2 будут немного отличаться друг от друга. Если теперь точку 2 приближать к точке 1, пересечение перпендикуляров O2 будет перемещаться вдоль прямой O21 и в пределе окажется в некоторой точке O1. Расстояния R1 и R2 будут стремиться к общему пределу R, равному радиусу кривизны, а точка O1 и будет центром кривизны для точки 1. Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту 1). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.
Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту 1). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.
Итак, в общем случае ускорение имеет две составляющие — тангенциальную
направленную вдоль касательной и определяющую скорость изменения модуля вектора скорости нормальную
направленную перпендикулярно скорости к центру кривизны траектории и пропорциональную угловой скорости вращения вектора скорости при движении частицы вдоль криволинейной траектории (рис. 2.14).
Рис. 2.14. Тангенциальное и нормальное ускорения при ускоренном криволинейном движении.
Действительно , где и есть угловая скорость вращения вектора скорости .
Полное ускорение
определяется по правилу параллелограмма. Модуль полного ускорения в соответствии с теоремой Пифагора равен
Модуль полного ускорения в соответствии с теоремой Пифагора равен
Выпишем без вывода формулы, связывающие радиус кривизны плоской траектории с координатами траектории. Если известна зависимость y = y(x), то
Если же траектория задана в параметрическом виде, x = x(t), y = y(t), то
Пример криволинейного движения с постоянным ускорением (тело, брошенное под углом к горизонту) приведен на следующем рисунке:
Рис. 2.15. Движение тела, брошенного под углом к горизонту
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно.
Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется
до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора,
то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость
То есть скорость
его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно,
пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется,
замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните,
скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени,
за который это изменении произошло. Определить среднее ускорение можно формулой:
где –
вектор ускорения.
Направление вектора ускорения совпадает с направлением изменения скорости
Δ = — 0
(здесь 0 – это начальная скорость,
то есть скорость, с которой тело начало ускоряться).
В момент времени t1 (см. рис 1.8) тело имеет скорость 0.
В момент времени t2 тело имеет скорость .
Согласно правилу вычитания векторов найдём вектор изменения скорости
Δ = — 0.
Тогда определить ускорение можно так:
Рис. 1.8. Среднее ускорение.
В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду
в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки,
при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами,
ускорение определяет, насколько изменяется скорость тела за одну секунду. Например,
если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду
увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени –
это физическая величина, равная пределу, к которому стремится среднее ускорение при
стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает
тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости
Δ при очень малых значениях промежутка времени,
за который происходит изменение скорости.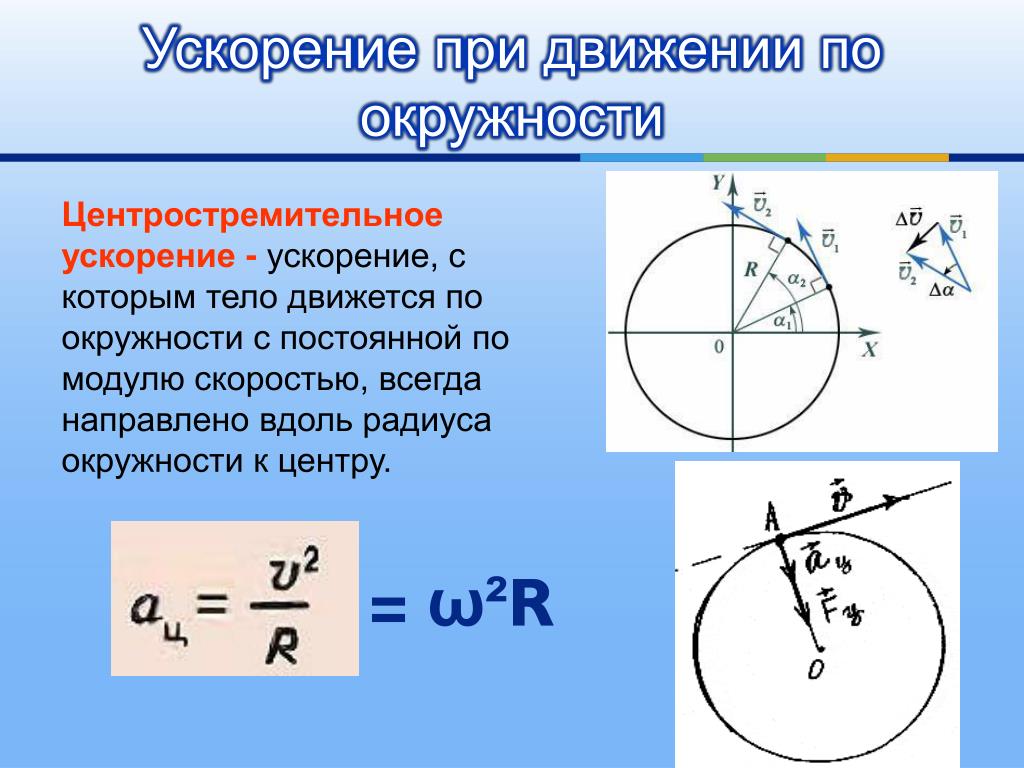 Вектор ускорения может быть задан проекциями
Вектор ускорения может быть задан проекциями
на соответствующие оси координат в данной системе отсчёта (проекциями аХ,
aY, aZ).
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1
а направление вектора ускорения совпадает с вектором скорости
2.
Если скорость тела по модулю уменьшается, то есть
v21
то направление вектора ускорения противоположно направлению вектора скорости
2. Иначе говоря,
в данном случае происходит замедление движения, при этом ускорение
будет отрицательным (а
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости,
но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих
(см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора
ускорения, направленная вдоль касательной к траектории в данной точке траектории движения.
Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения
τ
(см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения,
направленная вдоль нормали к траектории движения в данной точке на траектории движения тела.
То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10).
Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой
n.
Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального
и нормального ускорений по
правилу сложения векторов
и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется
правилом сложения векторов:
= τ + n
10.3 Связь угловых и поступательных величин — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Учитывая уравнение линейной кинематики, запишите соответствующее уравнение кинематики вращения
- Расчет линейных расстояний, скоростей и ускорений точек вращающейся системы с учетом угловых скоростей и ускорений
В этом разделе мы связываем каждую из вращательных переменных с поступательными переменными, определенными в Движении вдоль прямой линии и Движении в двух и трех измерениях. Это завершит нашу способность описывать вращения твердого тела.
Угловые и линейные переменные
В разделе «Переменные вращения» мы ввели угловые переменные. Если мы сравним определения вращения с определениями линейных кинематических переменных из «Движения по прямой линии» и «Движения в двух и трех измерениях», мы обнаружим, что имеет место отображение линейных переменных во вращательные. Линейное положение, скорость и ускорение имеют свои вращательные аналоги, как мы можем видеть, когда запишем их рядом:
Линейное положение, скорость и ускорение имеют свои вращательные аналоги, как мы можем видеть, когда запишем их рядом:
.
| Линейный | Вращательный | |
|---|---|---|
| Позиция | х | θθ |
| Скорость | v=dxdtv=dxdt | ω=dθdtω=dθdt |
| Ускорение | а=двдта=двдт | α=dωdtα=dωdt |
Давайте сравним линейные и вращательные переменные по отдельности. Линейная переменная положения имеет физические единицы измерения метры, тогда как переменная углового положения имеет безразмерные единицы измерения радианы, как видно из определения θ=srθ=sr, которое представляет собой отношение двух длин. Линейная скорость измеряется в м/с, а угловая скорость — в рад/с. В разделе «Вращательные переменные» мы видели, что в случае кругового движения линейная тангенциальная скорость частицы на радиусе r от оси вращения связано с угловой скоростью соотношением vt=rωvt=rω. Это также может относиться к точкам на твердом теле, вращающемся вокруг фиксированной оси. Здесь мы рассматриваем только круговое движение. При круговом движении, как равномерном, так и неравномерном, существует центростремительное ускорение (Движение в двух и трех измерениях). Вектор центростремительного ускорения направлен внутрь от частицы, совершающей круговое движение, к оси вращения. Вывод величины центростремительного ускорения дан в «Движении в двух и трех измерениях».
Линейная переменная положения имеет физические единицы измерения метры, тогда как переменная углового положения имеет безразмерные единицы измерения радианы, как видно из определения θ=srθ=sr, которое представляет собой отношение двух длин. Линейная скорость измеряется в м/с, а угловая скорость — в рад/с. В разделе «Вращательные переменные» мы видели, что в случае кругового движения линейная тангенциальная скорость частицы на радиусе r от оси вращения связано с угловой скоростью соотношением vt=rωvt=rω. Это также может относиться к точкам на твердом теле, вращающемся вокруг фиксированной оси. Здесь мы рассматриваем только круговое движение. При круговом движении, как равномерном, так и неравномерном, существует центростремительное ускорение (Движение в двух и трех измерениях). Вектор центростремительного ускорения направлен внутрь от частицы, совершающей круговое движение, к оси вращения. Вывод величины центростремительного ускорения дан в «Движении в двух и трех измерениях». Из этого вывода было найдено, что величина центростремительного ускорения равна
Из этого вывода было найдено, что величина центростремительного ускорения равна
ac=vt2r,ac=vt2r,
10,14
где r радиус окружности.
Таким образом, при равномерном круговом движении, когда угловая скорость постоянна, а угловое ускорение равно нулю, мы имеем линейное ускорение, то есть центростремительное ускорение, поскольку тангенциальная скорость в уравнении 10.14 является постоянной. Если присутствует неравномерное круговое движение, вращающаяся система имеет угловое ускорение, и мы имеем как линейное центростремительное ускорение, которое изменяется (поскольку изменяется vtvt), так и линейное тангенциальное ускорение. Эти соотношения показаны на рис. 10.14, где показаны центростремительные и тангенциальные ускорения для равномерного и неравномерного кругового движения.
Рисунок
10.14
(a) Равномерное круговое движение: вектор центростремительного ускорения acac направлен внутрь к оси вращения. Тангенциальное ускорение отсутствует. (b) Неравномерное движение по окружности: угловое ускорение создает внутреннее центростремительное ускорение, которое изменяется по величине, плюс тангенциальное ускорение atat.
(b) Неравномерное движение по окружности: угловое ускорение создает внутреннее центростремительное ускорение, которое изменяется по величине, плюс тангенциальное ускорение atat.
Центростремительное ускорение связано с изменением направления тангенциальной скорости, тогда как тангенциальное ускорение связано с любым изменением величины тангенциальной скорости. Векторы тангенциального и центростремительного ускорения a→ta→t и a→ca→c всегда перпендикулярны друг другу, как показано на рис. 10.14. Чтобы завершить это описание, мы можем сопоставить полный вектор линейного ускорения точке на вращающемся твердом теле или частице, совершающей круговое движение с радиусом r от фиксированной оси. Вектор полного линейного ускорения a→a→ представляет собой векторную сумму центростремительного и тангенциального ускорений,
a→=a→c+a→t.a→=a→c+a→t.
10.15
Суммарный вектор линейного ускорения в случае неравномерного кругового движения указывает на угол между центростремительным и тангенциальным векторами ускорения, как показано на рис. 10.15. Поскольку a→c⊥a→ta→c⊥a→t, величина полного линейного ускорения равна
10.15. Поскольку a→c⊥a→ta→c⊥a→t, величина полного линейного ускорения равна
|a→|=ac2+at2.|a→|=ac2+at2.
Обратите внимание, что если угловое ускорение равно нулю, общее линейное ускорение равно центростремительному ускорению.
Рисунок
10.15
Частица совершает круговое движение и имеет угловое ускорение. Полное линейное ускорение частицы представляет собой векторную сумму векторов центростремительного и тангенциального ускорений. Вектор полного линейного ускорения находится под углом между центростремительным и тангенциальным ускорениями.
Связь между вращательным и поступательным движением
Мы можем рассмотреть два соотношения между вращательным и поступательным движением.
- Вообще говоря, уравнения линейной кинематики имеют аналоги вращения. В таблице 10.2 перечислены четыре линейных кинематических уравнения и соответствующий вращательный аналог. Два набора уравнений выглядят похожими друг на друга, но описывают две разные физические ситуации, то есть вращение и перенос.

Ротационный Перевод θf=θ0+ω–tθf=θ0+ω–t х=x0+v–tx=x0+v–t ωf=ω0+αtωf=ω0+αt vf=v0+atvf=v0+at θf=θ0+ω0t+12αt2θf=θ0+ω0t+12αt2 xf=x0+v0t+12at2xf=x0+v0t+12at2 ωf2=ω02+2α(Δθ)ωf2=ω02+2α(Δθ) vf2=v02+2a(Δx)vf2=v02+2a(Δx) Стол
10.2Вращательные и поступательные кинематические уравнения
- Второе соответствие имеет отношение к линейным и вращательным переменным в частном случае кругового движения.
 Это показано в таблице 10.3, где в третьем столбце мы перечислили связующее уравнение, которое связывает линейную переменную с вращательной переменной. Вращательные переменные угловой скорости и ускорения имеют нижние индексы, указывающие на их определение в круговом движении.
Это показано в таблице 10.3, где в третьем столбце мы перечислили связующее уравнение, которое связывает линейную переменную с вращательной переменной. Вращательные переменные угловой скорости и ускорения имеют нижние индексы, указывающие на их определение в круговом движении.
Поворотный Трансляционный Связь (r=радиусr=радиус) θθ с θ=срθ=ср ωω втвт ω=vtrω=vtr αα на α=атрα=атр акак ак=vt2rac=vt2r Стол
10. 3
3Вращательные и поступательные величины: круговое движение
Пример
10,7
Линейное ускорение центрифуги
Центрифуга имеет радиус 20 см и разгоняется от максимальной скорости вращения 10 000 об/мин до остановки за 30 секунд при постоянном угловом ускорении. Он вращается против часовой стрелки. Какова величина полного ускорения точки на кончике центрифуги в момент времени t=29,0 с?t=29,0 с? Как направлен вектор полного ускорения?
Стратегия
Имея предоставленную информацию, мы можем рассчитать угловое ускорение, что затем позволит нам найти тангенциальное ускорение. Мы можем найти центростремительное ускорение в момент времени t=0t=0, рассчитав тангенциальную скорость в это время. Зная величины ускорений, мы можем вычислить общее линейное ускорение. Из описания вращения в задаче можно набросать направление вектора полного ускорения.
Решение
Угловое ускорение равно
α=ω−ω0t=0−(1,0×104)2π/60,0 с(рад/с)30,0 с=−34,9 рад/с2,α=ω−ω0t=0−(1,0×104)2π/60,0 с (рад/с) 30,0 с = −34,9 рад/с2.
Таким образом, тангенциальное ускорение равно
at=rα=0,2 м(−34,9 рад/с2)=−7,0 м/с2.at=rα=0,2 м(−34,9 рад/с2)=−7,0 м/с2.
Угловая скорость при t=29,0st=29,0 с равна
35,1 рад/с.ω=ω0+αt=1,0×104(2π60,0 с)+(−34,9 рад/с2)(29.0 с) = 1047,2 рад/с − 1012,71 = 35,1 рад/с.
Таким образом, тангенциальная скорость при t=29,0st=29,0 с равна
vt=rω=0,2 м(35,1 рад/с)=7,0 м/с. РС.
Теперь мы можем рассчитать центростремительное ускорение при t=29,0st=29,0с: =245,0 м/с2.
Поскольку два вектора ускорения перпендикулярны друг другу, величина полного линейного ускорения равна
|a→|=ac2+at2=(245,0)2+(−7,0)2=245,1 м/с2.|a →|=ac2+at2=(245,0)2+(−7,0)2=245,1 м/с2.
Поскольку центрифуга имеет отрицательное угловое ускорение, она замедляется. Общий вектор ускорения показан на рис. 10.16. Угол по отношению к вектору центростремительного ускорения равен
θ=tan−1−7,0245,0=−1,6°.θ=tan−1−7,0245,0=−1,6°.
Знак «минус» означает, что вектор полного ускорения направлен под углом по часовой стрелке.
Рисунок
10.16
Векторы центростремительного, тангенциального и полного ускорения. Центрифуга замедляется, поэтому тангенциальное ускорение направлено по часовой стрелке, против направления вращения (против часовой стрелки).
Значение
Из рисунка 10.16 мы видим, что вектор тангенциального ускорения противоположен направлению вращения. Величина тангенциального ускорения намного меньше центростремительного ускорения, поэтому вектор полного линейного ускорения будет составлять очень маленький угол по отношению к вектору центростремительного ускорения.
Проверьте свое понимание
10.3
Мальчик прыгает на карусели радиусом 5 м, находящейся в состоянии покоя. Он начинает разгоняться с постоянной скоростью до угловой скорости 5 рад/с за 20 секунд. Какое расстояние прошёл мальчик?
Интерактивный
Проверьте эту симуляцию PhET, чтобы изменить параметры вращающегося диска (начальный угол, угловая скорость и угловое ускорение) и разместить жуков на разных радиальных расстояниях от оси. Затем симуляция позволяет изучить, как круговое движение связано с xy положением, скоростью и ускорением жуков, используя векторы или графики.
Затем симуляция позволяет изучить, как круговое движение связано с xy положением, скоростью и ускорением жуков, используя векторы или графики.
Угловое ускорение | Физика
Цели обучения
К концу этого раздела вы сможете:
- Описать равномерное круговое движение.
- Объясните неравномерное круговое движение.
- Рассчитать угловое ускорение объекта.
- Соблюдайте связь между линейным и угловым ускорением.
Равномерное движение по окружности и гравитация обсуждали только равномерное движение по окружности, то есть движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Напомним, что угловая скорость ω была определена как скорость изменения угла θ :
[латекс]\omega =\frac{\Delta \theta}{\Delta t}\\[/latex]
, где θ — угол поворота, как показано на рисунке 1. Соотношение между угловой скоростью ω и линейной скоростью v также определяется в углах вращения и угловой скорости как
v = rω
или
[латекс]\ омега =\frac{v}{r} \\[/latex]
, где r — радиус кривизны, также показанный на рис. 1. Согласно соглашению о знаках, направление против часовой стрелки считается положительным направлением, а направление по часовой стрелке — отрицательным
1. Согласно соглашению о знаках, направление против часовой стрелки считается положительным направлением, а направление по часовой стрелке — отрицательным
Рисунок 1. На этом рисунке показано равномерное круговое движение и некоторые его определяемые величины.
Угловая скорость непостоянна, когда фигурист тянет руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается при выключении. Во всех этих случаях имеет место угловое ускорение , при котором изменяется ω . Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение α определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается следующим образом:
[латекс]\alpha =\frac{\Delta \omega }{\Delta t}\\[/latex],
где Δ ω — изменение угловой скорости и Δ t — изменение во времени. Единицы углового ускорения: (рад/с)/с или рад/с 2 . Если ω увеличивается, то α положительно. Если ω уменьшается, то α отрицательно.
Если ω увеличивается, то α положительно. Если ω уменьшается, то α отрицательно.
Пример 1. Расчет углового ускорения и замедления велосипедного колеса
Предположим, подросток кладет свой велосипед на спину и запускает вращение заднего колеса из состояния покоя до конечной угловой скорости 250 об/мин за 5,00 с. (a) Рассчитайте угловое ускорение в рад/с 2 . (b) Если теперь она ударит по тормозам, вызывая угловое ускорение -87,3 рад/с 2 , сколько времени понадобится колесу, чтобы остановиться?
Стратегия для (a)
Угловое ускорение можно найти непосредственно из его определения в [latex]\alpha =\frac{\Delta \omega }{\Delta t}\\[/latex] , потому что окончательный заданы угловая скорость и время. Мы видим, что ∆ ω — 250 об/мин, а Δ t — 5,00 с.
Решение задачи (a)
Введя известную информацию в определение углового ускорения, получим
[латекс]\begin{array}{lll}\alpha & =& \frac{\Delta \omega }{ \Delta t}\\ & =& \frac{\text{250 об/мин}}{\text{5,00 с}}\text{. {2}\text{.}\end{массив}\\[/latex]
{2}\text{.}\end{массив}\\[/latex]
Стратегия для (b)
В этой части мы знаем угловое ускорение и начальную угловую скорость. Мы можем найти время остановки, используя определение углового ускорения и решение для Δ t , что дает
[латекс]\Delta t=\frac{\Delta \omega}{\alpha}\\[/latex].
Решение для (b)
Здесь угловая скорость уменьшается с 26,2 рад/с (250 об/мин) до нуля, так что Δ ω равно –26,2 рад/с, и 9{2}}\\ & =& \text{0,300 с.}\end{array}\\[/latex]
Обсуждение
Обратите внимание, что угловое ускорение, когда девушка крутит колесо, небольшое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение большое и отрицательное. Угловая скорость быстро стремится к нулю. В обоих случаях отношения аналогичны тому, что происходит с линейным движением. Например, когда вы врезаетесь в кирпичную стену, происходит большое замедление — изменение скорости сильно за короткий промежуток времени.
Если бы велосипед в предыдущем примере стоял на колесах, а не в перевернутом положении, он сначала разогнался бы по земле, а затем остановился бы. Эту связь между круговым движением и линейным движением необходимо исследовать. Например, было бы полезно знать, как связаны линейное и угловое ускорения. При круговом движении линейное ускорение равно касательной к окружности в интересующей точке, как показано на рис. 2. Таким образом, линейное ускорение называется касательное ускорение a t .
Рис. 2. При круговом движении линейное ускорение a возникает при изменении величины скорости: a касается движения. В контексте кругового движения линейное ускорение также называют тангенциальным ускорением a t .
Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления. Мы знаем из равномерного кругового движения и гравитации, что при круговом движении центростремительное ускорение a c относится к изменениям направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рис. 3. Таким образом, a t и a c перпендикулярны и независимы друг от друга. Тангенциальное ускорение a t напрямую связано с угловым ускорением α и связано с увеличением или уменьшением скорости, но не ее направления.
Объект, совершающий круговое движение, испытывает центростремительное ускорение, как показано на рис. 3. Таким образом, a t и a c перпендикулярны и независимы друг от друга. Тангенциальное ускорение a t напрямую связано с угловым ускорением α и связано с увеличением или уменьшением скорости, но не ее направления.
Рис. 3. Центростремительное ускорение a c возникает при изменении направления скорости; оно перпендикулярно круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
Теперь мы можем найти точное соотношение между линейным ускорением a t и угловым ускорением α . Поскольку линейное ускорение пропорционально изменению величины скорости, оно определяется (как это было в одномерной кинематике) как
[латекс] {а} _ {\ текст {т}} = \ гидроразрыва {\ Delta v} {\ Delta t} \\ [/латекс].
Для кругового движения обратите внимание, что v = rω , так что
[латекс]{a}_{\text{t}}=\frac{\Delta \left(\mathrm{r\omega} \right)}{\Delta t}\\[/latex].
Радиус r является постоянным для кругового движения, поэтому Δ( rω ) = r (Δ ω ). Таким образом,
[латекс] {а} _ {\ текст {т}} = г \ гидроразрыва {\ дельта \ омега {\ дельта t} \\ [/латекс].
По определению, [латекс]\альфа =\фракция{\Дельта \омега }{\Дельта t}\\[/латекс]. Таким образом,
a t = rα ,
или
[латекс]\alpha =\frac{{a}_{\text{t}}}{r}\\[/latex]
9000 4 Эти уравнения означают, что линейное ускорение и угловое ускорение прямо пропорциональны. Чем больше угловое ускорение, тем больше линейное (тангенциальное) ускорение, и наоборот. Например, чем больше угловое ускорение ведущих колес автомобиля, тем больше ускорение автомобиля. Радиус тоже имеет значение. Например, чем меньше колесо, тем меньше его линейное ускорение при заданном угловом ускорении α .
Пример 2. Расчет углового ускорения колеса мотоцикла
Мощный мотоцикл может разгоняться от 0 до 30,0 м/с (около 108 км/ч) за 4,20 с. Каково угловое ускорение его колес с радиусом 0,320 м? (См. рис. 4.)
Рис. 4. Линейное ускорение мотоцикла сопровождается угловым ускорением его колес.
Стратегия
Нам дана информация о линейных скоростях мотоцикла. Таким образом, мы можем найти его линейное ускорение 9{2}\end{массив}\\[/латекс].
Обсуждение
Радианы безразмерны и появляются в любом соотношении между угловыми и линейными величинами.
До сих пор мы определили три величины вращения — θ, ω и α . Эти величины аналогичны поступательным величинам x, v и a . В таблице 1 показаны вращательные величины, аналогичные поступательные величины и отношения между ними.
| Поворотный | Трансляционный | Отношения |
|---|---|---|
| θ | х | [латекс]\тета =\фрак{х}{г}\\[/латекс] |
| ω | против | [латекс]\omega =\frac{v}{r}\\[/латекс] |
| α | а | [латекс]\alpha =\frac{{a}_{t}}{r}\\[/latex] |
Установление связей: домашний эксперимент
Сядьте, поставив ноги на землю, на вращающийся стул. Поднимите одну ногу так, чтобы она была разогнута (выпрямлена). Используя другую ногу, начните вращать себя, отталкиваясь от земли. Прекратите использовать ногу, чтобы отталкиваться от земли, но позвольте стулу вращаться. От исходной точки, с которой вы начали, зарисуйте угол, угловую скорость и угловое ускорение вашей ноги как функцию времени в виде трех отдельных графиков. Оцените величины этих величин.
Оцените величины этих величин.
Проверьте свое понимание
Угловое ускорение представляет собой вектор, имеющий как величину, так и направление. Как мы обозначаем его величину и направление? Проиллюстрируйте примером.
Решение
Величина углового ускорения равна α , а наиболее распространенными единицами измерения являются рад/с 2 . Направление углового ускорения вдоль фиксированной оси обозначается знаком + или -, так же как направление линейного ускорения в одном измерении обозначается знаком + или -. Например, рассмотрим гимнаста, выполняющего сальто вперед. Ее угловой момент был бы параллелен мату и слева от нее. Величина ее углового ускорения будет пропорциональна ее угловой скорости (скорости вращения) и ее моменту инерции относительно ее оси вращения.
Исследования PhET: Революция божьей коровки
Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.
Изучите, как круговое движение связано с положением жука по осям x, y, скоростью и ускорением, используя векторы или графики.
Нажмите, чтобы загрузить симуляцию. Запуск с использованием Java.
Резюме раздела
- Равномерное круговое движение — это движение с постоянной угловой скоростью [латекс]\омега =\фракция{\Delta \theta }{\Delta t}\\[/latex].
- При неравномерном круговом движении скорость изменяется со временем, а скорость изменения угловой скорости (т. е. углового ускорения) равна [латекс]\альфа =\фракция{\Delta \omega }{\Delta t}\\[/ латекс].
- Линейное или тангенциальное ускорение относится к изменениям величины скорости, но не ее направления, задается как [латекс] {а} _ {\ текст {t}} = \ гидроразрыва {\ Delta v} {\ Delta t} \\ [ /латекс].
- Для кругового движения обратите внимание, что [latex]v=\mathrm{r\omega }[/latex], так что
[латекс] {a} _ {\ mathrm {\ text {t}}} = \ frac {\ Delta \ left (\ mathrm {r \ omega} \ right)} {\ Delta t} \\ [/latex] .

- Радиус r постоянен для кругового движения, поэтому [латекс]\mathrm{\Delta}\left(\mathrm{r\omega}\right)=r\Delta \omega\\[/latex]. Таким образом,
[латекс] {a} _ {\ text {t}} = r \ frac {\ Delta \ omega {\ Delta t} \\ [/latex].
- По определению, [латекс]\Дельта\омега /\Дельта t=\альфа\\[/латекс]. Таким образом,
[латекс] {а} _ {\ текст {т}} = \ mathrm {г \ альфа} \\ [/латекс]
или
[латекс]\альфа =\фракция{{а}_{\текст{т}}}{г}\\[/латекс].
Концептуальные вопросы
1. Между вращательными и поступательными физическими величинами существуют аналогии. Определите вращательный термин, аналогичный каждому из следующих: ускорение, сила, масса, работа, поступательная кинетическая энергия, линейный импульс, импульс.
2. Объясните, почему центростремительное ускорение изменяет направление скорости при круговом движении, но не ее величину.
3. При круговом движении тангенциальное ускорение может изменить величину скорости, но не ее направление. Поясните свой ответ.
Поясните свой ответ.
4. Предположим, что кусок пищи находится на краю вращающейся плиты микроволновой печи. Испытывает ли он ненулевое тангенциальное ускорение, центростремительное ускорение или и то, и другое, когда: (а) Пластина начинает вращаться? б) Пластина вращается с постоянной угловой скоростью? в) Пластинка останавливается?
Задачи и упражнения
1. На пике смерч имеет диаметр 60,0 м и скорость ветра 500 км/ч. Какова его угловая скорость в оборотах в секунду?
2. Интегрированные концепции Ультрацентрифуга разгоняется из состояния покоя до 100 000 об/мин за 2,00 мин. а) Чему равно его угловое ускорение в рад/с 2 ? б) Каково тангенциальное ускорение точки на расстоянии 9,50 см от оси вращения? (c) Каково радиальное ускорение в м/с 2 и кратно g этой точки при полных оборотах в минуту?
3. Интегрированные концепции У вас есть точильный камень (диск) весом 90,0 кг, радиусом 0,340 м, вращающийся со скоростью 90,0 об/мин, и вы прижимаете к нему стальной топор с радиальной силой 20,0 Н.


 Это показано в таблице 10.3, где в третьем столбце мы перечислили связующее уравнение, которое связывает линейную переменную с вращательной переменной. Вращательные переменные угловой скорости и ускорения имеют нижние индексы, указывающие на их определение в круговом движении.
Это показано в таблице 10.3, где в третьем столбце мы перечислили связующее уравнение, которое связывает линейную переменную с вращательной переменной. Вращательные переменные угловой скорости и ускорения имеют нижние индексы, указывающие на их определение в круговом движении.  3
3 Вращательные и поступательные величины
Вращательные и поступательные величины