Марочник сталей и сплавов онлайн
Стали
Стандарты
Всего сталей
| Страна | Стандарт | Описание | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Россия | ГОСТ 5520-79 | Прокат листовой из углеродистой, низколегированной и легированной стали для котлов и сосудов, работающих под давлением. Технические условия Технические условия | ||||||||||
| Россия | ГОСТ 19821-83 | Затворы для фотоаппаратов. Основные параметры. Технические требования. Методы испытаний | ||||||||||
| Россия | ТУ 14-3-1573-96 | Трубы стальные электросварные прямошовные диаметром 530 — 1020 мм с толщиной стенки до 32 мм для магистральных газопроводов, нефтепроводов и нефтепродуктопроводов | ||||||||||
Химический состав 17ГС
Массовая доля элементов стали 17ГС по
ГОСТ 5520-79
| C (Углерод) | Si (Кремний) | Mn (Марганец) | P (Фосфор) | S (Сера) | Cr (Хром) | Ni (Никель) | Ti (Титан) | Al (Алюминий) | Cu (Медь) | N (Азот) | As (Мышьяк) | Fe (Железо) |
| 0,14 — 0,2 | 0,4 — 0,6 | 1,0 — 1,4 | остальное |
Массовая доля элементов стали 17ГС по
ГОСТ 19821-83
| C (Углерод) | Si (Кремний) | Mn (Марганец) | P (Фосфор) | S (Сера) | Cr (Хром) | V (Ванадий) | Nb (Ниобий) | Ti (Титан) | Al (Алюминий) | Cu (Медь) | N (Азот) | As (Мышьяк) | Fe (Железо) |
| 0,14 — 0,2 | 0,4 — 0,6 | 1,0 — 1,4 | остальное |
Механические свойства стали 17ГС
Свойства по стандарту ГОСТ 5520-79
|
Сортамент |
Категория |
Толщина, мм |
Предел текучести, σ0,2, МПа |
Временное сопротивление разрыву, σв, МПа |
Относительное удлинение при разрыве, δ5, % |
|
Лист |
2 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
3 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
4 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
5 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
6 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
10 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
11 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
12 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
16 |
12 — 20 |
335 |
490 |
23 |
|
Лист |
18 |
12 — 20 |
335 |
490 |
23 |
|
Лист |
19 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
20 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
21 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
|
Лист |
22 |
< 5 5 — 10 10 — 12 |
345 345 335 |
510 510 490 |
23 23 23 |
Испытания при повышенной температуре
|
Категория |
Температура, °С |
Предел текучести, σ0,2, МПа |
|
16 |
200 250 300 350 400 450 |
265 245 225 206 176 176 |
|
18 |
200 250 300 350 400 450 |
265 245 225 206 176 176 |
Испытание на ударный изгиб
|
Категория |
Толщина, мм |
Ударная вязкость, KCU, Дж/см2 |
|
Поперечные образцы с концентратором напряжений | ||
|
20 |
5 — 50 |
34,0 |
Свойства по стандарту ГОСТ 19821-83
|
Прокат |
Класс прочности |
Толщина, мм |
Предел текучести, σ0,2, МПа |
Временное сопротивление разрыву, σв, МПа |
Относительное удлинение при разрыве, δ5, % |
|
Листовой прокат и гнутые профили |
325 |
< 60 |
> 325 |
> 450 |
> 21 |
|
Листовой прокат и гнутые профили |
345 |
< 50 |
> 345 |
> 450 |
> 23 |
Свойства по стандарту
ТУ 14-3-1573-96
|
Сортамент |
Класс прочности |
Наружный диаметр, мм |
Толщина стенки, мм |
Предел текучести, σ0,2, МПа |
Временное сопротивление разрыву, σв, МПа |
Относительное удлинение при разрыве, δ5, % |
|
Трубы |
К52 |
530 |
7 — 16 |
> 350 |
510 — 630 |
> 20 |
|
Трубы |
К52 |
630 |
8 — 16 |
> 350 |
> 510 |
> 20 |
|
Трубы |
К52 |
720 |
8 — 16 |
> 350 |
> 510 |
> 20 |
|
Трубы |
К52 |
820 |
9 — 16 |
> 350 |
> 510 |
> 20 |
|
Трубы |
К52 |
1020 |
10 — 16 |
> 350 |
> 510 |
> 20 |
×
Отмена
Удалить
×
Выбрать тариф
×
Подтверждение удаления
Отмена
Удалить
×
Выбор региона будет сброшен
Отмена
×
×
Оставить заявку
×
| Название | |||
Отмена
×
К сожалению, данная функция доступна только на платном тарифе
Выбрать тариф
Сталь 17ГС: Расшифровка марки | ООО «Сталь-Максимум»
Главная
Справочник
Марки сталей
17ГС
|
Марка стали |
Вид поставки
Сортовой и фасонный прокат, полоса, гнутые профили – ГОСТ 19281–89. | |||||||||||||||||||||||||||||||||||||||||
|
17ГС | ||||||||||||||||||||||||||||||||||||||||||
|
Массовая доля элементов, % |
НД |
Температура критических точек, ºС | ||||||||||||||||||||||||||||||||||||||||
|
С |
Si |
Mn |
S |
P |
Cr |
Ni |
As |
N |
Cu |
Ас1 |
Ас3 |
Аr1 |
Аr3 | |||||||||||||||||||||||||||||
|
0,14–
0,20 |
0,40–
0,60 |
1,00–
1,40 |
≤
0,040 |
≤
0,035 |
≤
0,30 |
≤
0,30 |
≤
0,08 |
≤
0,008 |
≤
0,30 |
ГОСТ
5520–79 |
745 |
870 |
680 |
790 | ||||||||||||||||||||||||||||
|
≤
0,012 |
ГОСТ
19281–89 | |||||||||||||||||||||||||||||||||||||||||
|
Механические свойства при комнатной температуре | ||||||||||||||||||||||||||||||||||||||||||
|
НД |
Режим термообработки |
Сечение,
мм |
σ0,2,
Н/мм2 |
σВ,
Н/мм2 |
δ,
% |
Ψ,
% |
KCU,
Дж/см2 |
KCU, после механи-ческого старения, Дж/см2
|
Изгиб
| |||||||||||||||||||||||||||||||||
|
Операция |
t, ºС |
Охлаждающая
среда |
не менее
| |||||||||||||||||||||||||||||||||||||||
|
ГОСТ
5520–79 |
Термическая обработка |
До 5
От 5 до
10
От 10 до 20 |
345
345
335 |
510
510
490 |
23
23
23 |
–
–
|
–
441
341 |
–
29
29 | ||||||||||||||||||||||||||||||||||
|
От 4 до
20 |
d=3,5а | |||||||||||||||||||||||||||||||||||||||||
|
ГОСТ
19281–89 |
Листовой и широкополосный прокат в горячекатаном или термически
обработанном состоянии
|
До 5 |
345 |
490 |
23 |
– |
64
391
292 |
29 |
d=2а | |||||||||||||||||||||||||||||||||
|
От 5
до 10 |
345 |
490 |
23 |
–
|
64
391
292 |
29 |
d=2а | |||||||||||||||||||||||||||||||||||
|
От 10 до 20 |
325 |
450 |
23 |
– |
291
292
403
404 |
29 |
d=2а
| |||||||||||||||||||||||||||||||||||
|
Гнутые профили в горячекатаном или термически обработанном состоянии
|
До 10
От 10 до 20
|
345
325 |
490
450 |
23
23 |
–
– |
–
– |
–
– |
d=2а | ||||||||||||||||||||||||||||||||||
|
1 KCU при минус 40 ºС.
2 KCU при минус 70 ºС.
3 KCV при 0 ºС.
4 KCV при минус 20 ºС.
Требования к механическим свойствам и ударной вязкости (за исключением KCV) листового проката установлены для поперечных образцов. | ||||||||||||||||||||||||||||||||||||||||||
|
Назначение. Днища, фланцы, корпусы аппаратов и другие сварные детали, работающие под давлением при температуре до 350 ºС в котлах и трубопроводах и при температурах от минус 40 ºС до 475 ºС в сосудах. Электросварные трубы трубопроводов пара и горячей воды с температурой 425 ºС (прямошовные) и 350 ºС (спиральношовные) и давлением до 2,5 Н/мм2. | ||||||||||||||||||||||||||||||||||||||||||
|
Предел
выносливости,
Н/мм2 |
Термообработка |
Ударная вязкость, KCU, Дж/см2,
при t, ºС |
Термообработка | |||||||||||||||||||||||||||||||||||||||
|
σ-1 |
τ-1 |
+ 20 |
0 |
– 20 |
– 40 |
– 60 |
–80 | |||||||||||||||||||||||||||||||||||
|
Технологические характеристики | ||||||||||||||||||||||||||||||||||||||||||
|
Ковка |
Охлаждение поковок, изготовленных | |||||||||||||||||||||||||||||||||||||||||
|
Вид полуфабриката |
Температурный
интервал ковки, ºС |
из слитков |
из заготовок | |||||||||||||||||||||||||||||||||||||||
|
Размер сечения, мм |
Условия охлаждения |
Размер сечения, мм |
Условия охлаждения | |||||||||||||||||||||||||||||||||||||||
|
Слиток | ||||||||||||||||||||||||||||||||||||||||||
|
Заготовка | ||||||||||||||||||||||||||||||||||||||||||
|
Свариваемость |
Обрабатываемость резанием |
Флокеночувствительность | ||||||||||||||||||||||||||||||||||||||||
|
Ограниченно свариваемая.
Способы сварки: РД, РАД, АФ, МП, ЭШ и КТ. Рекомендуются подогрев и последующая термообработка.
|
В термически обработанном состоянии при
σВ = 460 Н/мм2
К√ = 1,84 (твердый сплав),
К√ = 1,7 (быстрорежущая сталь) |
Не чувствительна | ||||||||||||||||||||||||||||||||||||||||
|
Склонность к отпускной хрупкости | ||||||||||||||||||||||||||||||||||||||||||
|
Не склонна | ||||||||||||||||||||||||||||||||||||||||||
Другие стали низколегированные
Оставьте заявку и получите
актуальные цены и сроки поставки
Ответим в течение 15 минут. Предложение будет у вас в течение 24 часов
Отправляя форму, я соглашаюсь с политикой о персональных данных
Красивое авиационное искусство.
 Часть третья |
Часть третья |
Мы продолжаем серию из шести частей, чтобы продемонстрировать некоторые из лучших картин, изображающих важные события воздушной войны Второй мировой войны:
Направляясь в Токио, подполковник Джимми Дулиттл запускает свой B-25 Mitchell с вздымающейся палубы авианосца USS. «Хорнет», утро 18 апреля 1942 года. Возглавляя группу из шестнадцати бомбардировщиков в их дальнем полете в один конец, «Рейдеры Дулитла» нанесли первый удар в самое сердце имперской Японии после печально известного нападения на Перл-Харбор четырьмя месяцами ранее. Вместе они совершили один из самых дерзких воздушных налетов в истории авиации.
Самый результативный летчик-истребитель в истории Эрих Хартманн сбивает свою последнюю жертву, свой 352-й советский истребитель Як-9 над Брно в Словакии. Здесь изображен Хартманн, пилотирующий свой Messerschmitt ME109 «Черный тюльпан» 8 мая 1945 года, в последний день войны.
«Тележки, высота 11 часов!» — закричал лейтенант Дуг Каннинг, нарушив двухчасовое радиомолчание. 18 апреля майор Джон Митчелл повел шестнадцать P-38 из своей 339-й истребительной эскадрильи с Хендерсон-Филд на Гуадалканале на Бугенвиль.43 для перехвата бомбардировщика Betty, на борту которого находился командующий Объединенным флотом Японии адмирал Исороку Ямамото. Теперь, пролетев 400 миль на высоте 50 футов над водой, ориентируясь по чистому счислению пути, самолет заметил два бомбардировщика Betty в сопровождении шести Zeroe, снижающихся к острову Баллале.
18 апреля майор Джон Митчелл повел шестнадцать P-38 из своей 339-й истребительной эскадрильи с Хендерсон-Филд на Гуадалканале на Бугенвиль.43 для перехвата бомбардировщика Betty, на борту которого находился командующий Объединенным флотом Японии адмирал Исороку Ямамото. Теперь, пролетев 400 миль на высоте 50 футов над водой, ориентируясь по чистому счислению пути, самолет заметил два бомбардировщика Betty в сопровождении шести Zeroe, снижающихся к острову Баллале.
Майор Митчелл и двенадцать «Лайтнингов» поднялись наверх, чтобы обеспечить высокое укрытие, в то время как капитан Том Ланфьер и лейтенанты. Рекс Барбер, Фрэнк Холмс и Рэй Хайн, назначенные «штурмовиком», развернулись, чтобы перехватить бомбардировщики. Когда они поднимались к Бетти, Ланфьер увидел трех Зеро, пикирующих, чтобы защитить бомбардировщики, и резко повернулся к ведущему истребителю, предоставив Барберу продолжить атаку на бомбардировщик.
Обогнув головной бомбардировщик, Барбер прострелил снижающуюся Бетти от крыла до крыла. Из правого двигателя повалил густой черный дым, и бомбардировщик рванул влево. Через несколько мгновений он врезался в джунгли, место крушения было отмечено поднимающимся столбом черного маслянистого дыма.
Из правого двигателя повалил густой черный дым, и бомбардировщик рванул влево. Через несколько мгновений он врезался в джунгли, место крушения было отмечено поднимающимся столбом черного маслянистого дыма.
Повернув к побережью, Барбер прикончил вторую Бетти, которую теперь атаковал Фрэнк, и сбил Зеро, который с опозданием вступил в бой с близлежащего аэродрома Кахили. Вскоре после этого Митчелл заявил: «Миссия выполнена!» и пятнадцать «Лайтнингов» повернули к Гуадалканалу. Лейтенант Рэй Хайн, которого в последний раз видели скользящим по воде с дымом, тянущимся из его двигателя, не вернулся с задания и так и не был найден.
Этот экстраординарный перехват, осуществленный P-38, базировавшимися недалеко от Гуадалканала, стал возможен благодаря усилиям по радиоперехвату и расшифровке сигналов разведывательными службами ВМФ в Перл-Харборе и других точках Тихого океана.
Немецкие реактивные истребители Me 262, которые в начале 1945 года использовались в основном для атаки соединений тяжелых бомбардировщиков ВВС США, были очень уязвимы для атак истребителей во время взлета и посадки. Поэтому союзники адаптировали стратегию патрулирования истребителями вблизи баз Me262 в ожидании возвращения немецких самолетов с их миссий. Эти засады вскоре оказались очень эффективными: Люфтваффе потеряло много самолетов из-за орудий ВВС США.
Поэтому союзники адаптировали стратегию патрулирования истребителями вблизи баз Me262 в ожидании возвращения немецких самолетов с их миссий. Эти засады вскоре оказались очень эффективными: Люфтваффе потеряло много самолетов из-за орудий ВВС США.
Чтобы противодействовать растущим потерям, были сформированы специальные подразделения, оснащенные Focke-Wulf 190 D-9 («Дора Нойн»), которые многие считают лучшим поршневым истребителем Люфтваффе войны. Управляемые опытными ветеранами JG52 и JG54, им было поручено обеспечить верхнее прикрытие самолетов на их аэродромах в Мюнхене и Айнринге недалеко от Зальцбурга.
Для того, чтобы эти самолеты были хорошо заметны немецким зенитчикам, их днище было окрашено в красный цвет с белыми полосами, так родилась легенда о «крыле попугая». Одним из элементов этого подразделения был так называемый «рой душителей» во главе с лейтенантом Хейно Заксенбергом.
Здесь мы видим Заксенберга в его Focke Wulf 190 Dora 9 «Rote 1» W.Nr. 600424, когда он превращается в P-51 над аэродромом Айнринг, пытаясь защитить приближающиеся реактивные истребители от атаки «Мустангов».
В 14:00 9 февраля 1945 года 31 истребитель Bristol Beaufighter из 445-й (RAAF), 404-й (RCAF) и 144-й эскадрилий (RAF) поднялся в воздух для удара по небольшому военно-морскому флоту Германии, скрытому в Фордефьорде. К 19:00 того же вечера 404-я эскадрилья смирилась с потерей шести своих самолетов, 11 убитыми и одним военнопленным. Всего в тот день было потеряно девять истребителей Bristol Beaufighter и один североамериканский Mustang. Немцы потеряли 5 фокке-вульфов 190 с. Четырнадцать членов экипажа союзников и два немецких пилота погибли.
Конец лета 1940 года, Битва за Британию в самом разгаре. Гоняясь к побережью после бомбардировки южной Англии, He111 из KG55 был атакован Спитфайром истребительного командования Королевских ВВС. Бомбардировщик сильно поврежден, но в самый последний момент пара Me109 из JG26 приходит на помощь, отправляя «Спитфайр» в Ла-Манш. Если им повезет, экипаж «Хейнкеля» еще может вернуться на свою базу во Франции.
Утром 25 мая 1944 года трое пилотов из 4-й истребительной группы «Дебден Иглз» 336-й истребительной эскадрильи 8-й воздушной армии находились над Германией в поисках неприятностей. Пролетая возле Ботенхайма, они столкнулись с немецкими самолетами из III JG1 9-го штаба.
Пролетая возле Ботенхайма, они столкнулись с немецкими самолетами из III JG1 9-го штаба.
Во время завязавшегося воздушного боя самолет Messerschmitt Bf109G-6/AS (также известный как Ausburg Eagle) приблизился к P-51B Mustang капитана Джозефа Х. Беннетта, оставаясь ниже порыва пропеллера P-51.
Орудия Bf109 заклинило, но молодой пилот Люфтваффе оберфенрих Хуберт Хекманн был полон решимости не дать американскому летчику уйти. Хекманн подъехал на высоту Р-51 и протаранил свой Bf109.истребитель в хвост самолета Беннета.
Удар оторвал хвостовую часть и хвостовую часть фюзеляжа и оказался в нескольких футах от бака хвостовой части фюзеляжа.
Подняв нос своего самолета к небу, Беннет катапультировался недалеко от Ботенхайма. Зайдя в петлю, Р-51 врезался в дом посреди поселка. Его собственный самолет серьезно поврежден, Хекманну удалось совершить аварийную посадку на брюхо.
Беннетт, бывший пилот эскадрильи Королевских ВВС Eagle, был схвачен и доставлен в тюрьму немецкими военными. Позже Хекманн приехал, чтобы представиться и познакомиться с первым американским летчиком, которого он вывел из строя. Беннет остается немецким военнопленным до конца войны. 336-я истребительная эскадрилья потеряла в этом бою еще один «Мустанг», но заявила, что сбила пять самолетов противника.
Позже Хекманн приехал, чтобы представиться и познакомиться с первым американским летчиком, которого он вывел из строя. Беннет остается немецким военнопленным до конца войны. 336-я истребительная эскадрилья потеряла в этом бою еще один «Мустанг», но заявила, что сбила пять самолетов противника.
После войны два летчика подружились и каждый год встречались, чтобы воссоединиться.
Возглавляемые командиром эскадрильи Роландом «Би» Бимонтом «Тайфуны» Hawker из 609-й эскадрильи наглядно показаны, когда они поднимаются со своей базы в Мэнстоне в апреле 1943 года. Галерея Второй мировой войны Национального музея авиации и космонавтики, Смитсоновский институт, Вашингтон, округ Колумбия.
B-17G, 42-38050, «Птица грома» 303-й бомбардировочной группы, базирующейся в Молсуорте, Англия, замечен в 11:45, 15 августа 1944, над Триром, Германия, по возвращении на базу после миссии в Вайсбадене. B-17G «Bonnie B», «Special Delivery» и «Marie» видны ниже, когда Messerschmitt 109G и Focke Wulf FW 190 атакуют элемент Thunder Bird.
Исследования Джеффа Этелла для фрески выявили имена и идентификационные номера самолетов всех американских и многих немецких участников этого сражения, в котором 303-й полк потерял девять крепостей в этой атаке истребителей Люфтваффе.
Не пропустите четвертую часть «Прекрасного авиационного искусства».
Криптоанализ с N-граммами — Математика ∩ Программирование
Этот пост является третьим в серии постов о вычислениях с наборами данных на естественном языке. Первые два сообщения см. в соответствующем разделе нашей основной страницы контента.
Немного детской забавы
В этом посте мы сосредоточимся на проблеме декодирования шифров подстановки. Во-первых, мы опишем несколько методов, которые люди используют для взлома шифров. Мы найдем их неудовлетворительными и перейдем к упрощенному алгоритму, который выполняет локальный поиск в пространстве всех возможных расшифровок, где мы используем наш алгоритм сегментации слов из прошлого раза, чтобы определить вероятность того, что расшифровка верна. Мы продолжим тенденцию этой серии работать на Python, чтобы мы могли повторно использовать наш код из предыдущих постов. Наконец, мы поэкспериментируем, запустив код на реальных шифрах подстановки, которые использовались в истории. А в следующий раз поработаем над улучшением алгоритма поиска на скорость и точность. Как обычно, весь код, использованный в этом сообщении в блоге, доступен на странице этого блога в Github.
Мы продолжим тенденцию этой серии работать на Python, чтобы мы могли повторно использовать наш код из предыдущих постов. Наконец, мы поэкспериментируем, запустив код на реальных шифрах подстановки, которые использовались в истории. А в следующий раз поработаем над улучшением алгоритма поиска на скорость и точность. Как обычно, весь код, использованный в этом сообщении в блоге, доступен на странице этого блога в Github.
Итак, приступим.
Определение : Сообщение, которое может прочитать человек, называется незашифрованным текстом , а зашифрованное сообщение называется зашифрованным текстом .
Когда я был еще мальчишкой, мне нравилось разгадывать головоломки из одной книги о долгих автомобильных поездках. Мне не удалось найти книгу на Amazon, но каждая страница представляла собой очередную известную цитату, запутанную шифром подстановки, и целью читателя было расшифровать цитату вручную. Другими словами, каждая головоломка предоставляла зашифрованный текст, и вам нужно было найти соответствующий открытый текст. Большинство людей интуитивно понимают идею шифра подстановки, но мы также можем четко определить его с помощью терминологии из нашего поста о метриках слов. (Если вас пугает слово «моноид», пропустите математическое определение и сначала прочитайте приведенный ниже пример.) 9{-1}(w_{\textup{enc}})$. Заметим, что $\bar{f}$ однозначно определяется $f$, так что проблема расшифровки сообщения сводится к определению правильного ключа.
Большинство людей интуитивно понимают идею шифра подстановки, но мы также можем четко определить его с помощью терминологии из нашего поста о метриках слов. (Если вас пугает слово «моноид», пропустите математическое определение и сначала прочитайте приведенный ниже пример.) 9{-1}(w_{\textup{enc}})$. Заметим, что $\bar{f}$ однозначно определяется $f$, так что проблема расшифровки сообщения сводится к определению правильного ключа.
Чтобы объяснить это простым английским языком, ключ подстановки представляет собой одностороннее сопоставление букв английского алфавита. Например, мы могли бы перевести A в G, B в S, C в Q и т. д., но мы могли бы передать A в G, а G не обязательно переходить в A. При шифровании открытого текстового сообщения мы просто заменяем каждый A с G, каждый B с S, и так далее, пока мы не посчитаем каждую букву в сообщении. Вышеприведенное условие «биекции» просто означает, что каждая буква связана с какой-то другой буквой, и нет конфликта ассоциаций (например, мы не можем иметь, чтобы и A, и B были связаны с L, потому что это привело бы к множественным расшифровкам). *}$. Таким образом, дважды применяя метод шифрования, мы фактически возвращаем исходное текстовое сообщение. Но, конечно, циклический шифр слишком упрощен; как правило, ключ подстановки может сопоставлять любые две буквы вместе, чтобы сделать код более сложным.
*}$. Таким образом, дважды применяя метод шифрования, мы фактически возвращаем исходное текстовое сообщение. Но, конечно, циклический шифр слишком упрощен; как правило, ключ подстановки может сопоставлять любые две буквы вместе, чтобы сделать код более сложным.
Расшифровка шифров подстановки в моем детском сборнике головоломок включала в себя несколько приемов, которые при комбинировании и применении (более или менее случайным образом) скорее всего давали правильное расшифровывание. К ним относятся:
- Рассматривание однобуквенных слов и выбор I, A, а иногда и O в качестве замены.
- Глядя на короткие слова из двух букв и слов из трех букв и пробуя такие слова, как «to», «an» и «the» вместо них. Другими словами, частично расшифруйте часть текста и посмотрите, не приведет ли использование этой частичной замены к абсурдному расшифровыванию других частей сообщения.
- Поиск сдвоенных букв и замена их обычными сдвоенными буквами, такими как «ee», «tt», «ss», «ff» и «ll»
- Найдите наиболее часто встречающуюся букву и попробуйте заменить ее обычными буквами, такими как e, s, t, r, l или n.

К сожалению, большинство из них в значительной степени зависят от нескольких отговорок. Во-первых, текст из этой книги-головоломки включал знаки препинания, пробелы между словами и другие отличительные черты английского языка. В реальной жизни шифры обычно представляют собой один толстый блок текста или разделены на блоки фиксированной ширины; при правильной расшифровке естественная способность человека к сегментации слов делает сообщение очевидным. Во-вторых, я заранее знал, что открытое текстовое сообщение было известной цитатой! У меня была внутренняя информация о содержании сообщения, поэтому расшифровать его было легче. Часто закодированное сообщение не является полным предложением, и часто люди, выполняющие шифрование, удаляют общие слова, но все же сохраняют смысл расшифрованной фразы (например, «высадка в полночь, бар, черный ход»). Кроме того, текст может преднамеренно содержать орфографические ошибки и другие виды фальсификации сообщения, чтобы избежать расшифровки.
Другими словами, сообщения в книге головоломок были безупречны, и их было легко разгадать. Мы больше заинтересованы в разработке решателя, который сохраняет качество в условиях несовершенства и обмана.
При этом шаблоны, которые мы использовали в детстве, дают представление о том, как мы можем построить алгоритм для расшифровки сообщений. При ручном расшифровывании часто можно было очень близко подойти к решению и заметить, что две буквы заменены неправильно, но остальная часть сообщения верна. Переворачивая неправильно подставленные буквы, можно было прийти к правильной расшифровке и похлопать себя по плечу. Это ключ к следующему алгоритму, поскольку мы начнем со случайной расшифровки и постепенно улучшаем ее, пока не сможем больше этого делать. Но прежде чем мы туда доберемся, нам нужно выяснить, как правильно представить наши данные.
Представление шифра в виде фрагмента данных
Один из простых способов представления ключа шифра очень похож на приведенный выше пример: просто используйте 26-символьную строку букв, например «nopqrstuvwxyzabcdefghijklm», где мы предполагаем, что буква «а» соответствует к первому символу строки, ‘b’ ко второму и так далее. Это представление пригодится нам позже, когда мы захотим внести небольшие коррективы в ключ: мы можем просто поменять местами любые две буквы в списке или выполнить перестановки троек букв.
Это представление пригодится нам позже, когда мы захотим внести небольшие коррективы в ключ: мы можем просто поменять местами любые две буквы в списке или выполнить перестановки троек букв.
Теперь, когда у нас есть ключ, мы можем разработать функцию, которая шифрует сообщение. В Python мы используем приятные строковые методы для замены символов:
import string алфавит = "abcdefghijklmnopqrstuvwxyz" def encrypt(msg, ключ): return msg.translate(string.maketrans(алфавит, ключ))
Метод перевода строки очень специфичен: для его работы требуется таблица переводов из всего алфавита ASCII 256 символов. Чтобы облегчить настройку этого для относительно простых переводов, Python предоставляет нам функцию «maketrans», которая при задании входного и выходного алфавита создает таблицу перевода, в которой i-й символ первого аргумента преобразуется в i-й символ второго аргумента, а все остальное оставляет без изменений. Обратите внимание, что здесь мы не включаем заглавные буквы. Заинтересованный читатель может увидеть исходный код для незначительных модификаций, исправляющих заглавные буквы; это не очень интересно, поэтому мы опускаем его здесь.
Заинтересованный читатель может увидеть исходный код для незначительных модификаций, исправляющих заглавные буквы; это не очень интересно, поэтому мы опускаем его здесь.
Например, с помощью следующего ключа мы можем зашифровать некоторые тестовые сообщения:
>>> key = "qwertyuiopasdfghjklzxcvbnm"
>>> encrypt("почему привет", ключ)
'vin itssg zitkt' И функция расшифровки очень похожа:
def decrypt(msg, key): return msg.translate(string.maketrans(key, Alphabet))
Убедитесь, что расшифровка приведенного выше зашифрованного сообщения работает должным образом:
>>> decrypt("vin itssg zitkt", key)
'почему привет' Далее нам нужно уметь «вертеть» ключ. Наш окончательный алгоритм будет начинаться со случайного ключа и постепенно улучшаться, меняя две буквы за раз. Для этого мы можем снова использовать ту же функцию «перевода»:
def keySwap(key, a, b): return key.translate(string.maketrans(a+b, b+a))
Другими словами, если буква $x$ отображается в $a$, а $y$ отображается в $b$, то это Функция возвращает ключ, который отображает $x$ в $b$ и $y$ в $a$. Итак, теперь, когда у нас есть представление для ключа, давайте выясним, как «сделать ключ лучше».
Итак, теперь, когда у нас есть представление для ключа, давайте выясним, как «сделать ключ лучше».
Буквенные триграммы
Наша общая стратегия такова: начните со случайного ключа, а затем придумайте какой-нибудь способ судить о ключе на основе его расшифровки. Оттуда поменяйте местами пары букв в ключе, чтобы посмотреть на ключи, которые «рядом». Если какой-либо обмен признан лучшим, чем текущий ключ, используйте его в качестве нового ключа и начните процесс заново. Мы перестаем искать новые ключи через определенное количество шагов, либо получаем расшифровку с определенным уровнем точности.
Этот алгоритм является общей парадигмой оптимизации. Обычное название — «самый крутой спуск» или «самый крутой подъем», и аналогия очевидна. Предположим, мы хотим добраться до вершины высочайшей вершины Тибета. Мы можем начать с какого-нибудь случайного места в Тибете и осмотреться вокруг. Если мы стоим рядом с местом, которое выше, чем сейчас, переместитесь в это место и повторите. Очевидно, что в этом алгоритме есть некоторые проблемы: во-первых, мы всегда попадаем на какой-то пик, но можем и не попасть на 9-ю вершину.0061 самый высокий пик. Чтобы облегчить это, мы можем запустить алгоритм из большого количества случайных начальных точек и сравнить все пики, к которым мы пришли. Конечно, при наличии достаточного количества случайных начальных точек мы, скорее всего, найдем самый высокий пик (в конце концов, мы случайным образом начнем с на — самой цели или, по крайней мере, очень близко к ней!). Во-вторых, если бы мы попробовали этот алгоритм в Иллинойсе, мы могли бы вообще никогда не найти холмов! Это оставило бы нас вслепую блуждающими по кукурузному полю и явно пустой тратой времени. Прежде чем мы приступим к какой-либо работе, мы должны иметь четкое представление о том, что пространство, которое мы ищем, больше похоже на Тибет, чем на Иллинойс, и желательно, чтобы у нас был только один главный пик.
Очевидно, что в этом алгоритме есть некоторые проблемы: во-первых, мы всегда попадаем на какой-то пик, но можем и не попасть на 9-ю вершину.0061 самый высокий пик. Чтобы облегчить это, мы можем запустить алгоритм из большого количества случайных начальных точек и сравнить все пики, к которым мы пришли. Конечно, при наличии достаточного количества случайных начальных точек мы, скорее всего, найдем самый высокий пик (в конце концов, мы случайным образом начнем с на — самой цели или, по крайней мере, очень близко к ней!). Во-вторых, если бы мы попробовали этот алгоритм в Иллинойсе, мы могли бы вообще никогда не найти холмов! Это оставило бы нас вслепую блуждающими по кукурузному полю и явно пустой тратой времени. Прежде чем мы приступим к какой-либо работе, мы должны иметь четкое представление о том, что пространство, которое мы ищем, больше похоже на Тибет, чем на Иллинойс, и желательно, чтобы у нас был только один главный пик.
Итак, наше описание «близких» ключей действительно таково. Вспоминая наш первый пост из серии о метриках слов, мы хотим исследовать удачно подобранные ключи, близкие к заданному ключу по метрике Левенштейна. Используя аналогию, мы ищем, какие направления выше в 26 измерениях, поэтому мы не можем искать во всех направлениях увеличение. Вместо этого мы хотим заранее знать, какие направления, скорее всего, будут выше, и проверять только эти направления. Мы сейчас увидим, как это сделать.
Вспоминая наш первый пост из серии о метриках слов, мы хотим исследовать удачно подобранные ключи, близкие к заданному ключу по метрике Левенштейна. Используя аналогию, мы ищем, какие направления выше в 26 измерениях, поэтому мы не можем искать во всех направлениях увеличение. Вместо этого мы хотим заранее знать, какие направления, скорее всего, будут выше, и проверять только эти направления. Мы сейчас увидим, как это сделать.
Самая трудная часть, на самом деле, это определение «ценности» данной расшифровки. Основная проблема является одной из основных проблем во всей этой серии: как мы можем определить, является ли строка символов разумным языком? С одной стороны, если мы знаем, что это разумно, мы можем сегментировать его. Мы позаботились об этом в прошлый раз. Но как узнать, является ли строка символов осмысленной?
Конечно, точный ответ на этот вопрос выходит далеко за рамки этого поста, но оказывается, что разумные 9н$.
Обратите внимание, что с большим объемом интернет-текста (как мы говорили в разделе о сегментации слов) мы можем вычислить количество троек букв. Снова заимствовав со страницы Норвига, у нас есть список буквенных триграмм и буквенных биграмм. В файлах встречаются все возможные 2-граммы и 3-граммы, и вот пример наиболее распространенных и наименее распространенных из обоих:
Снова заимствовав со страницы Норвига, у нас есть список буквенных триграмм и буквенных биграмм. В файлах встречаются все возможные 2-граммы и 3-граммы, и вот пример наиболее распространенных и наименее распространенных из обоих:
Для биграмм:
в 134812613554 133210262170 э 119214789533 повторно 108669181717 он 106498528786 ... кв 60 zq 6170496 джх 5682177 QZ 4293975 jq 2858953
И триграммы:
82103550112 43727954927 и 43452082914 ион 39907843075 тио 32705432538 энт 31928292897 ... 10340 8871 zqy 8474 jzq 7180 zgq 6254
Обратите внимание, что даже если мы не различаем сами слова, истинная расшифровка определенно будет содержать общие триграммы и биграммы, но если наш ключ неверен, вероятно (просто случайно) некоторые необычные триграммы и биграммы в полученная расшифровка. Таким образом, мы можем взять набор всех буквенных триграмм в последовательности, вычислить вероятность случайного появления каждой триграммы и взять произведение всех из них, чтобы получить оценку для данной расшифровки.
Реализация: наискорейший подъем и генерация соседей
Алгоритм наискорейшего подъема практически одинаков для любой задачи. На псевдо-питоне это выглядит примерно так:
def крутойАсцент(posn, AssessmentPosn, generateNeighbors, numSteps):
val = оценитьPosn(posn)
соседи = generateNeighbors (posn)
для я в numSteps:
следующий = соседи.следующий()
nextVal = оценитьPosn (следующий)
если следующее значение > значение:
значение = следующее значение
поз = следующий
соседи = generateNeighbors (далее)
обратная позиция Итак, нам нужна функция, которая генерирует соседей данной позиции, и функция оценки. Прежде чем мы действительно напишем реальную реализацию нашего алгоритма наискорейшего восхождения для ключей дешифрования, давайте напишем функцию оценки, а затем функцию для генерации соседних ключей.
Во-первых, чтобы оценить качество расшифровки, нам нужна функция, извлекающая все буквенные триграммы. Мы можем сделать это в общем случае для буквенных n-грамм:
Мы можем сделать это в общем случае для буквенных n-грамм:
def letterNGrams(msg, n): вернуть [msg[i:i+n] для i в диапазоне (len(msg) - (n-1))]
Теперь вспомните класс, который мы разработали в посте о сегментации слов, который загружает файл с подсчетом слов и вычисляет вероятности. Как оказалось, мы можем повторно использовать этот код для загрузки любого файла, где в каждой строке есть слово и число. Итак, с небольшой модификацией и включением мы импортируем алгоритм сегментации слов из прошлого раза (это включено в нашу реализацию на странице Github этого блога. Незначительные изменения см. в файле segment.py).
Другими словами, чтобы загрузить наш файл слов триграммы, мы просто создаем экземпляр объекта, а затем используем тот же вид логарифмической суммы, что и для сегментации слов:
trigramLetterProb = OneGramDist('count-3l.txt')
Def trigramStringProb (msg):
возвращаемая сумма (math.log10 (trigramLetterProb (триграмма))
для триграммы в letterNGrams(msg, 3)) Таким образом, наша вышеприведенная функция «evaluatePosn» будет простой функцией «trigramStringProb». Чтобы привести пример этого:
Чтобы привести пример этого:
>>> trigramStringProb("hellotherefriend")
-42,624229232
>>> x = [зашифровать("привет друг",
перетасован (алфавит)) для i в диапазоне (20)]
>>> y = [(z,trigramStringProb(z)) для z в x]
>>> для (a,b) в y:
... напечатать("%s, %f" % (а,б))
...
зуаайфзуруориуеб, -75.711233
ejzzfgejljmlsjwk, -90,312349
ghnnctghshisuhoe, -64.815609
ikggrzikykfyqkld, -91.449079
аххукакфктфйкдо, -89.589869
гайынвгарарпадль, -68.828649
поттгипоаовакосб, -68.253187
hozznjhowolwuobx, -81.541286
ihuusoihnhvnrhyl, -78.413089
dmqquldmbmcbnmyk, -81.434687
амввтвамомкозмфр, -76.938938
znddfwznunjuhnie, -76.856587
rxddemrxkxuktxla, -82.547184
tjddsktjxjoxfjun, -83.725443
wxbbcdwxjxvjhxsy, -95.146985
hsvvonhsasgamspc, -66.135361
инаавдинонеомнгл, -59.646548
tcjjpxtcbcqbkcov, -88.000009
бурпвбуюайгуск, -75.768519
fkmmbxfkvkqvyknl, -94.509938 Итак, мы видим, что за неправильные расшифровки балл на порядки меньше: они, естественно, содержат много неупотребительных буквенных триграмм.
Для генерации соседних ключей мы также используем n-граммы, но на этот раз работаем с биграммами. Идея такова: взять самую необычную биграмму, найденную при попытке расшифровки сообщения, и исправить ключ, заменив биграмму более распространенной биграммой.
Делаем это довольно постепенно, в том смысле, что если мы видим, скажем, «xz», мы можем заметить, что «ez» встречается чаще, и просто поменять местами x и e в ключе. Таким образом, мы не всегда пытаемся заменить все необычные биграммы на «th» или «in». В коде:
bigramLetterProb = OneGramDist('count-2l.txt')
определить соседние ключи (ключ, расшифрованное сообщение):
биграммы = отсортированные (letterNGrams (decryptedMsg, 2),
ключ=bigramLetterProb)[:30]
для c1, c2 в биграммах:
для в перетасовке (алфавит):
если c1 == c2 и bigramLetterProb(a+a) >
bigramLetterProb(c1+c2):
yield keySwap (ключ, а, с1)
еще:
если bigramLetterProb(a+c2) > bigramLetterProb(c1+c2):
yield keySwap (ключ, а, с1)
если bigramLetterProb(c1+a) > bigramLetterProb(c1+c2):
yield keySwap (ключ, а, с2)
пока верно:
yield keySwap (ключ, random. choice (алфавит),
случайный.выбор(алфавит))
choice (алфавит),
случайный.выбор(алфавит)) Во-первых, мы создаем таблицу поиска вероятностей букв биграммы, как и в случае с триграммами. Чтобы сгенерировать соседние ключи, сначала мы сортируем все биграммы в слове так, чтобы наименее распространенные были первыми, а затем берем первые 30 из них. Затем перемешиваем алфавит (чтобы не смещать начало алфавита) и ищем улучшения в ключе. Обратите внимание, что эта функция является итератором. Другими словами, он не «возвращает» значение в том смысле, что останавливает выполнение. Вместо этого он «выдает» значение до тех пор, пока вызывающая сторона не запросит другое (с помощью функции «next()»), а затем возвращается к своим вычислениям, пока не достигнет другого результата. Таким образом, нам не нужно заранее генерировать огромный список ключей и рисковать тем, что они никогда не будут использованы. Вместо этого мы готовим новые ключи по запросу и вычисляем только то количество, которое необходимо. Поскольку мы часто находим лучший ключ в течение первых нескольких итераций, это, несомненно, сэкономит нам много ненужных вычислений. Наконец, исчерпав наш список из 30 наименее распространенных биграмм, мы делаем случайные замены, надеясь на улучшение.
Наконец, исчерпав наш список из 30 наименее распространенных биграмм, мы делаем случайные замены, надеясь на улучшение.
Обратите внимание, что для этой функции требуется и ключ, и расшифрованное сообщение. Это внешне изменяет наш алгоритм наискорейшего восхождения, потому что функция generateNeighbors требует два аргумента. Мы также изменили все имена переменных, чтобы они соответствовали этой проблеме.
по определению крутой подъем (сообщение, ключ, дешифрованиефитнес, количество шагов):
расшифровка = расшифровка (сообщение, ключ)
значение = decryptionFitness (расшифровка)
соседи = iter(neighboringKeys(ключ, расшифровка))
для шага в диапазоне (numSteps):
следующийКлюч = соседи.следующий()
nextDecryption = расшифровать (msg, nextKey)
следующее значение = decryptionFitness (следующее дешифрование)
если следующее значение > ценить:
ключ, расшифровка, значение = nextKey, nextDecryption, nextValue
соседи = iter(neighboringKeys(ключ, расшифровка))
print((расшифровка, ключ))
вернуть расшифровку
Обратите внимание, что мы также распечатываем частичные результаты, чтобы пользователь мог визуально увидеть промежуточные варианты клавиш. Теперь самый последний шаг — запустить код на нескольких случайных начальных ключах и собрать, сегментировать и отобразить результаты:
Теперь самый последний шаг — запустить код на нескольких случайных начальных ключах и собрать, сегментировать и отобразить результаты:
def shuffled(s):
sList = список(и)
random.shuffle(sList)
вернуть ''.join(sList)
деф preprocessInputMessage (символы):
return ''.join(re.findall('[az]+', chars.lower()))
def CrackSubstitution(msg, numSteps = 5000, перезапусков = 30):
msg = preprocessInputMessage(msg)
startKeys = [перемешено (алфавит) для i в диапазоне (перезапуск)]
localMaxes = [steepestAscent (msg, key, trigramStringProb, numSteps)
для ключа в startKeys]
для x в localMaxes:
печать (сегментWithProb (x))
prob, words = max(segmentWithProb(decryption) для расшифровки в localMaxes)
вернуть ' .join(слова) Сначала мы предварительно обрабатываем сообщение, чтобы убедиться, что все символы в нижнем регистре (мы удаляем все остальное), а затем генерируем группу случайных начальных ключей, выполняем самый крутой подъем по этим ключам и отображаем результаты вместе с наиболее вероятными, как выбираются путем сегментации слов. Давайте посмотрим, как это работает в реальном мире.
Давайте посмотрим, как это работает в реальном мире.
Немцы и русские: расшифрованы настоящие коды
Давайте попробуем запустить наш код на тестовом сообщении:
>>> msg = 'ujejvzrqfeygesvsoofsujwigfeestgufvvzgujjejcfwf\ qfevlgwvswpzsizfnasvvgeswnqfevrpfovfyswnqafigfvqegisogarv\ zgoflgljlgwvfxgfkvsckaxkvtfikjkoozjpnseafeestgufvvzgujje' >>> CrackSubstitution(msg) [... много вывода...] Говорят, что Дороти Паркер однажды подошла к двери квартиру, в которой проходила блестящая вечеринка в точно в тот же момент красивая, но бессмысленная танцовщица прибыл в дверь'
Помимо того, что они были правильными, большинство попыток также были очень близкими, давая первым буквам такие расшифровки, как «coroti» или «gorothy». Попробуем посложнее. Это сообщение было отправлено бароном Августом Шлюгой, немецким шпионом в Первой мировой войне (источник):
>>> msg = 'NKDIFSERLJMIBFKFKDLVNQIBRHLCJUKFTFLKSTENYQNDQNT\ TEBTTENMQLJFSNOSUMMLQTLCTENCQNKREBTTBRHKLQTELCBQQBSFSKLTMLS\ SFAINLKBRRLUKTLCJUKFTFLKFKSUCCFRFNKRYXB' >>> CrackSubstitution(msg) [... много вывода...] 'Англичане жалуются на нехватку боеприпасов, о которых они сожалеют что обещанная поддержка французского нападения к северу от аррас не возможен из-за боеприпасов недостаточность wa'
Вот код, присланный Олдричем Эймсом, самым известным кротом ЦРУ, которого когда-либо ловили. Это была часть сообщения, отправленного в 1992 году, которое было обнаружено у него при аресте:
>>> msg = 'cnlgvqvelhwttailehotweqvpcebtqfjnppedmfmlfcyfsqf\ spndhqfoeutnpptppctdqnifsqdtwhtnhhlfjolfsdhqfedhegnqtwvnqht\ nhhlfjwebbitspthdtxqqfoeutyfslfjedefdnifsqgnlngnpcttqedoedf\ gqfitlxni' >>> CrackSubstitution(msg) ... 'Parch Third Weez Bridge с кучей для массовой информации о вас нам и дать задницы, потраченные на новый де-ад-ром землю чтобы указать, какой de add rom будет использоваться дальше, чтобы дать твой миньон о каракасе пиет в октябре хаб'
Это немного более обескураживает, потому что очевидно близко к правильному, но не совсем так. Человек может быстро исправить ошибки, поменяв местами p на m, z и k. При этом, возможно, немного увеличив количество шагов, мы могли бы найти правильный путь к расшифровке.
При этом, возможно, немного увеличив количество шагов, мы могли бы найти правильный путь к расшифровке.
Вот еще одно письмо из того же источника, отправленное генералом Конфедерации Дж. Э. Джонстоном во время осады Виксбурга 25 мая 1863 года во время Гражданской войны в США. Оно было перехвачено, а затем расшифровано командой криптоаналитиков Линкольна из трех человек:0003
>>> msg = 'AKMSSROOHDCRDSMCRVRORGDWTHDRPBGRDORWRUUNGFHPGYGQ\ WTRNTCGYGQPTRDLPTHAHOPKGQPHTGWMDCWTHKHROPTHHDHFYHDNMFIHCWTM\ PROYGQKEGKHBHBGTDOPGDXM' >>> CrackSubstitution(msg) ... 'x raff отправляется в отдел fa, когда он придет в po in si \ вы, что вы думаете, что х есть маршрут, как и где находится \ вражеский лагерь whatisyourorepepohnstonja'
Опять же, мы близко, но не совсем там. На самом деле, на этот раз при расшифровке не удается сегментировать даже последний блок, даже если внутри него есть полезные фрагменты. Это побочный эффект нашей усердной модели сегментации, которая экспоненциально наказывает неизвестные слова по их длине.
К сожалению, наша программа чаще дает сбой, чем успех. Действительно, алгоритм не так уж и хорош. Можно надеяться, что следующая функция обычно идентифицирует любое данное сообщение, но это редко:
def testDecryption(msg): CrackSubstitution(encrypt(msg, shuffled(alphabet)))
На самом деле я еще не видел ни одного примера, чтобы эта функция возвращала разумный вывод для любого ввода.
>>> testDecryption("быстрая коричневая лиса перепрыгнула \
ленивая собака")
...
'Пладьюсигбвиклименизируетхмурится'
>>> testDecryption("я люблю математику и компьютер\
программирование")
...
'типлазма плазоуранкутлдиспедеаллонх'
>>> testDecryption("пришло время моржу сказать \
говорить о многих вещах о кораблях и обуви и сургуча \
капусты и короли почему море кипит и стоит ли\
у свиней есть крылья")
...
'Тив пошевелил теленка, сказал, чтобы срыгнуть что-нибудьсуширы\
а также обувь и герметик
Последнее было близко , но все же довольно далеко. Более того, для случайных небольших входных данных функция, кажется, генерирует разумный результат!
Более того, для случайных небольших входных данных функция, кажется, генерирует разумный результат!
>>> testDecryption("slkfhlakjhahlaweirhurv")
[... некоторый вывод...]
'l some store test and he chi' Не обращая внимания на удовольствие, которое мы могли бы получить, расшифровывая случайное сообщение, мы кричим: «Что дает?!» Кажется, здесь играет роль какая-то мера энтропии, и сообщения с меньшей энтропией имеют большее количество интерпретаций. Здесь энтропия может означать количество букв, используемых в сообщении, число различных букв, используемых в сообщении, или их комбинация.
Последнее очевидное раздражение состоит в том, что программа действительно медленная. Если мы понаблюдаем за промежуточными вычислениями, то заметим, что иногда оно будет приближаться к правильному решению, а затем отклоняться. Более того, количество шагов за прогон фиксировано. Почему бы ему не основываться на уже достигнутом прогрессе, продвинув эти близкие решения немного дальше к правильному ключу, возможно, потратив больше времени только на эти успешные расшифровки.
В следующий раз мы потратим время, пытаясь улучшить алгоритм наискорейшего подъема. Мы постараемся сделать так, чтобы быстрее отказывались от паршивых стартовых позиций, и выжимали максимум из удачных заездов. Далее мы проведем некоторую дополнительную обработку при поиске соседних ключей и потенциально задействуем 2-, 3-, 4- и даже 5-граммы букв.
Но в целом получилось неплохо. Мы часто подчеркиваем недостатки наших алгоритмов, но здесь у нас на удивление много преимуществ. Во-первых, мы действительно расшифровали сообщения из реальной жизни! Имея в руках эту программу, даже всего двадцать лет назад у нас был бы ценный инструмент для раскрытия гнусных секретов, закодированных с помощью подстановки.
Более того, благодаря нашему решению, основанному на данных, мы по своей сути усиливаем наш алгоритм дополнительной безопасностью. Это стабильный , в том смысле, что незначительное повреждение данных (возможно, опечатка или гнусное обфускация сообщения) обрабатывается хорошо: наш алгоритм сегментации допускает опечатки, и сообщение с одной или двумя опечатками по-прежнему имеет высокий балл буквенной триграммы в нашем вероятностная модель.

 Лист – ГОСТ 5520–79, ГОСТ 19281–89, ТУ 14–1–5241–93.
Лист – ГОСТ 5520–79, ГОСТ 19281–89, ТУ 14–1–5241–93.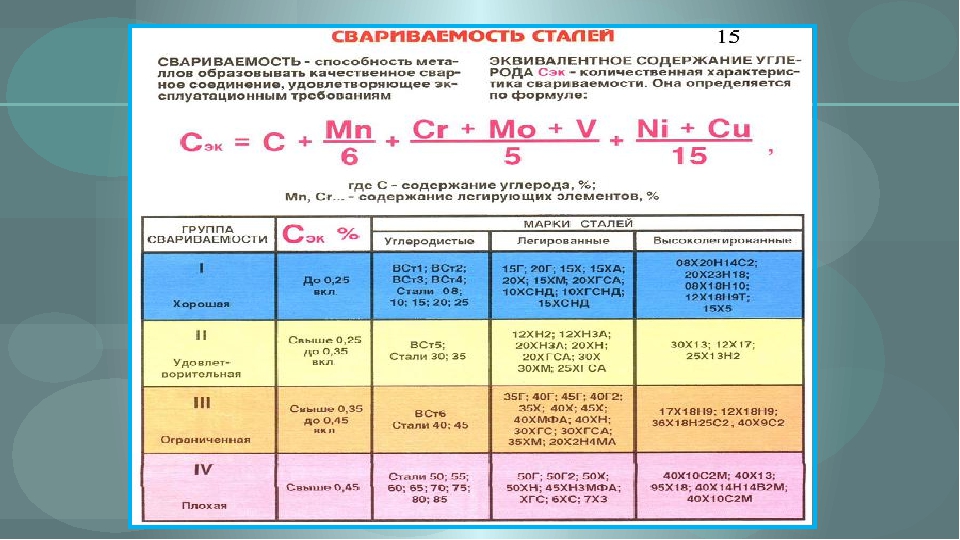


 choice (алфавит),
случайный.выбор(алфавит))
choice (алфавит),
случайный.выбор(алфавит))  .. много вывода...]
'Англичане жалуются на нехватку боеприпасов, о которых они сожалеют
что обещанная поддержка французского нападения к северу от
аррас не возможен из-за боеприпасов
недостаточность wa'
.. много вывода...]
'Англичане жалуются на нехватку боеприпасов, о которых они сожалеют
что обещанная поддержка французского нападения к северу от
аррас не возможен из-за боеприпасов
недостаточность wa'